Resistência ao corte segundo a ACI 318-19 no RFEM 6

Introdução

Na norma anterior ACI 318-14 {%>c - sem considerar os limites de aplicação. O utilizador pode escolher entre um método de cálculo simplificado e um exato. Um dos objetivos do novo conceito na norma ACI 318-19 era reduzir as equações de dimensionamento para V_c. Além disso, o conceito deve considerar a influência da altura do componente, a relação da armadura longitudinal e da tensão normal.

Resistência ao corte V_c De acordo com ACI 318-19

For non-prestressed reinforced concrete beams, the shear resistance V_c is calculated according to ACI 318-19 [1] with Equations a) to c) from Table 22.5.5.1. With the new Equations b) and c), the member height, the longitudinal reinforcement ratio, and the normal stress now influence the shear strength, V_c. Equation a) was basically taken from ACI 318-14 [2].

The determination of the shear resistance V_c according to Table 22.5.5.1 [1], depends on the inserted shear reinforcement A_v. Se a armadura de corte mínima A_{v, min} de acordo com 9.6.3.4 estiver disponível ou for excedida, o cálculo de V_c pode ser realizado de acordo com a Equação a)

ou a Equação b)

from Table 22.5.5.1 [1].
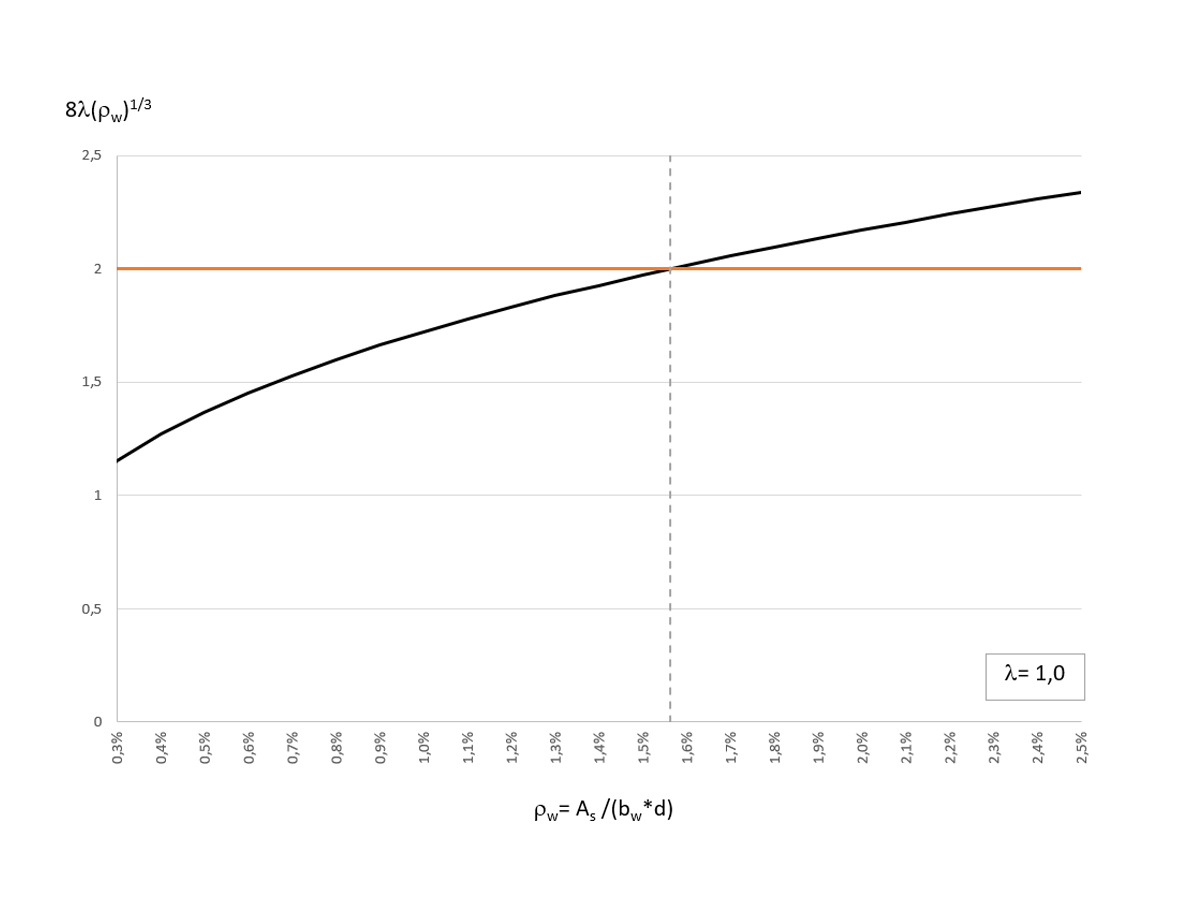
If you compare the two equations shown above, you can see that in Equation b), the factor 2 λ has been replaced by the term 8 λ (ρ_w)1/3. A relação de armadura longitudinal ρ_w influencia o cálculo da resistência de corte V_c. Image 01 shows the distribution of 8 λ (ρ_w)1/3 as a function of ρ_w (with λ = 1).

Para λ = 1,0, 8 λ (ρ_w ) ^1/3 torna-se igual ao valor 2 λ para uma relação de armadura longitudinal ρ_w = 1,56%. When calculating V_c, Equation a) for λ= 1 and a longitudinal reinforcement ratio ρ_w (greater than) 1.56% and Equation b) for λ= 1 and ρ_w > 1.56% results in the greater concrete shear resistance. The standard allows the application of both equations. Therefore, the maximum value from Equations a) and b) can be used for a cost-effective design.

For beams with shear reinforcement A_v less than A_v,min, Equation c) of Table 22.5.5.1 [1] is to be used according to ACI 318-19 [1].

Exceto para a variável λ_s , a equação c) é semelhante à equação b) discutida acima. For structural components with little or no shear reinforcement, the concrete shear resistance V_c decreases with increasing structural component height. Através da introdução do fator λ_s' é considerado o "Efeito de tamanho". The factor λ_s is determined according to Equation 22.5.5.1.3 [1] as follows.

The reduction of the shear resistance V_c,c by the factor λ_s is only effective for structural heights d (greater than) 10in. Image 02 shows the distribution of term 8 λ_s λ (ρ_w)^1/3 for the different effective depths d.

Exemplo: Calcular a armadura de corte necessária de acordo com a ACI 318-19

The following section describes how to determine the required shear reinforcement according to the new concept of ACI 318-19 [1] for a reinforced concrete beam, which was designed in a previous Knowledge Base Article according to ACI 318-14 [2]. Image 03 shows the structural model and the design load.

The rectangular cross-section has the dimensions 25 in. · 11 in. The concrete has a compressive strength of f'_c = 5,000 psi. The yield strength of the reinforcing steel used is f_y = 60,000 psi. The effective depth of the tension reinforcement is applied with d = 22.5 in. The design value of the acting shear force V_u at a distance d from the support is 61.10 kips.

The determination of the shear resistance V_s according to Table 22.5.5.1 [1] depends on the height of the inserted shear reinforcement A_v. The prerequisite for using Equations a) and b) is that the minimum shear reinforcement according to 9.6.3.4 [1] is applied. For this reason, a check is performed in the first step as to whether a minimum reinforcement has to be considered according to 9.6.3.1 [1].

61,10 kips > 13,13 kips

Isso requer uma armadura de corte mínima. This is calculated according to 9.6.3.4 [1], as follows.

a_{v, min} = 0,12 in²/ft

When considering the minimum shear reinforcement, the concrete shear resistance V_c can now be determined with Equations a) or b) of Table 22.5.5.1 [1]. The shear resistance V_c,a according to Equation a) is calculated as V_c,a = 35.0 kips. To apply Equation b), it is necessary to know the longitudinal reinforcement ratio ρ_w. To be able to compare the calculated shear reinforcement with the calculation result of the Concrete Design Add-on, ρ_w is determined with the required longitudinal reinforcement at the distance d from the support. A bending moment of M_y,u = 1533 kip-in results in a longitudinal reinforcement of A_s,req = 1.33 in², which is ρ_w = 0.536%. Image 01 shows the influence of the longitudinal reinforcement ratio ρw on the calculation of V_c,b. Since ρ_w (less than) 1.5% here, Equation b) will result in a lower shear resistance V_c,b than Equation a) and we can skip determining V_c,b. However, we calculate V_c,b to show it.

V_{c, b} = 24,52 kips

Conforme esperado, a Equação b) fornece uma resistência ao corte menor do que a Equação a).

Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1].
a_v,min = 0.12 in²/ft

When considering the minimum shear reinforcement, the concrete shear resistance V_c can now be determined with Equations a) or b) of Table 22.5.5.1 [1].

A resistência ao corte V_{c, a} de acordo com a Equação a) é calculada como V_{c, a} = 35,0 kips.

Para aplicar a Equação b), é necessário conhecer a relação de armadura longitudinal ρ_w. To be able to compare the calculated shear reinforcement with the calculation result of the Concrete Design Add-on, ρ_w is determined with the required longitudinal reinforcement at the distance d from the support. A bending moment of M_y,u = 1533 kip-in results in a longitudinal reinforcement of A_s,req = 1.33 in², which is ρ_w = 0.536%. Image 01 shows the influence of the longitudinal reinforcement ratio ρ_w on the calculation of V_c,b. Since ρ_w (greater than) 1.5% here, Equation b) will result in a lower shear resistance V_c,b than Equation a) and we can skip determining V_c,b. However, we calculate V_c,b to show it.

V_{c, b} = 24,52 kips

Conforme esperado, a Equação b) fornece uma resistência ao corte menor do que a Equação a).

Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1].

V_{c, max} = 87,5 kips

Finalmente, o cálculo da armadura de corte necessária resulta na seguinte resistência da força de corte do betão V_c.

V_c = máx [V_{c, a} ; V_{c, b} ] ≤ V_{c, max}

V_c = [35,0 kips; 24,5 kips] ≤ 87,5 kips

V_c = 35,0 kips

The required shear reinforcement req. a_v is calculated as follows:

Req. a_v = 0.41 in²/ft ≥ 0.12 in²/ft

The reinforced concrete design according to ACI 318-19 [1] can be performed with RFEM 6. The Concrete Design Add-on also calculates a required shear reinforcement of 0.43 in²/ft at the distance d from the support (see Image 04).

Atenção: The results in RFEM 6 differ from the hand calculations slightly due to a more accurate value for the Depth (d) calculated. RFEM 6 takes into account that there are multiple layers of tension reinforcement where the hand calculations assume a single layer.

Finalmente, a capacidade de carga máxima da escora de compressão do betão da treliça de corte é verificada de acordo com a Secção 22.5.1.2.

61.10 kips ≤ 175.00 kips.

A verificação de corte de acordo com ACI 318-19 é cumprida.
Conforme esperado, a Equação b) fornece uma resistência ao corte menor do que a Equação a).

Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1].

Resumo

ACI 318-19 [1] introduced a new concept to determine the shear resistance V_c. Foi possível reduzir o número de equações de dimensionamento potencial da versão anterior para três equações, tendo em consideração a influência da tensão normal, da altura do componente e da taxa de armadura longitudinal. Isto simplifica o cálculo da resistência ao corte V_c.