Obliczenia sztywności ścian odnoszą się do drugiego artykułu z tej serii.
.png?mw=760&hash=411141ff4b218660021601e7d879bf7f085db5d3)
1
Budynek
rzut kondygnacji
Zróżnicowana sztywność ścian ma znaczny wpływ na całkowite odkształcenie rzutu budynku. Ponadto asymetryczne rozmieszczenie ścian także wpływa na odkształcenie całego obiektu.
Zazwyczaj efekt ten jest uwzględniany w sztywnościach pozycji 2D.
Przykład
Efekt ten pokazano na prostym, dwukondygnacyjnym budynku. Rzut budynku jest regularny. Więcej informacji na temat kryteriów minimalnego usztywnienia można znaleźć w [1].
1
Budynek
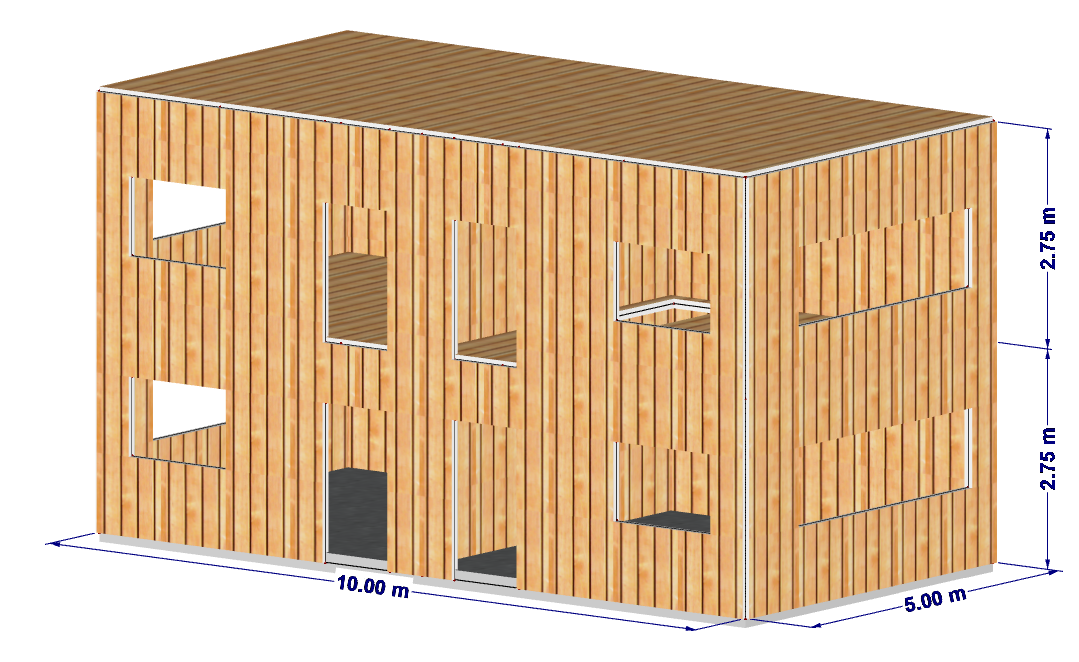
System
- Rzut podstawy = 5 m ⋅ 10 m
- Uproszczone obliczenia, wykluczone są okna na wysokościach kondygnacji.
- Na obu końcach ściany znajduje się ściąg.
- Konstrukcja ściany i sztywności zgodnie z opisem w drugim artykule tej serii.
- rozmiar siatki ES = 1,5 m
.png?mw=760&hash=90d1265dab7978f24ef548a08c67540ec50c89df)
2
Rzut
obciążenie konstrukcji
- Ciężar własny i konstrukcja = 2 kN/m²
- Obciążenie wiatrem w globalnym kierunku y
- WZ2
- Wysokość = 100 m n.p.m. NN
- we+ d = 0,46 + 0,74 = 1,2 kN/m²
- We, d = 1,2 kN/m² ⋅ 3 m = 3,6 kN/m
.png?mw=760&hash=e394494b7ce45447662696f68720e109cb244cfa)
Kombinacja
- KO1 = 1,0 PO1 + 1,5 PO2
Sztywności ścian
W rezultacie powstają cztery różne długości ścian. Dla uproszczenia obliczane są sztywności ścian dla prętów zastępczych. Wyznaczanie sztywności odbywa się w taki sam sposób, jak w poprzednim artykule.
| Ściana usztywniająca | Długość [m] | Moduł sprężystości [kN/cm²] | D66/D77 [kN/cm] | Moduł G [kN/cm²] | D88 [kN/cm] | Podpora pod względem sztywności [kNcm/rad] |
|---|---|---|---|---|---|---|
| 1 | 0,5 | 792 | 9,504 | 0,47 | 6.5 | 64,499 |
| 2 | 1,0 | 396 | 4,752 | 0,80 | 11,0 | 257,995 |
| 3 | 1,5 | 264 | 3,168 | 1,04 | 14,3 | 580,489 |
| 4 | 2,5 | 158 | 1,901 | 1,36 | 18,8 | 1.612.469 |
Sztywności ściany są obliczane dla każdej z czterech długości ściany. W tym celu na każdą ścianę nakłada się obciążenie jednostkowe 1 kN. Ponieważ ściany o długości powyżej 2,5 m i wysokości 2,75 m nie są możliwe do wyprodukowania, ściana środkowa jest dzielona w środku.
.png?mw=760&hash=cb7110a790a026249ac6b2b6d2b5658af1451bd9)
W załączonym pliku modelu RFEM nr 1 odkształcenia dla wszystkich długości ściany są obliczane jako powierzchnie i wyniki prętów. W górnej części modelu obliczane są odkształcenia bez kotwy, a w dolnej części z kotwą. Odkształcenia są również porównane na rysunku 04.
Na podstawie wyznaczonych odkształceń poszczególnych ścian obliczana jest sztywność dla każdej ściany.
Dla przykładu, dla ściany 1 o długości 50 cm uzyskuje się następującą sztywność:
C = F/u = 1 kN/22,5 mm = 0,044 kN/mm
c = F/l ⋅ C = 1 kN/0,5 m ⋅ 0,044 kN/mm = 0,088 N/mm²
Dla wszystkich ścian:
- Ściana | l = 0,5 m² | c = 0,088 N/mm²
- Ściana | l = 1,0 m² | c = 0,164 N/mm²
- Ściana | l = 1,5 m² | c = 0,230 N/mm²
- Ściana | l = 2,5 m² | c = 0,333 N/mm²
Sztywności te są przypisane do odpowiedniej podpory liniowej w rzucie (patrz Rysunek 05). Rzut znajduje się w załączonym pliku modelu RFEM 2.
.png?mw=760&hash=b6d7deeab4d8f4e66cee7c7eec2bf9f8a8a3c9aa)
Ze względu na to, ze budynek jest symetryczny, kondygnacja nie ulega obrotowi. Ten artykuł wyjaśnia to bardziej szczegółowo:
Załączony film wideo pokazuje, w jaki sposób siły poziome rozkładają się w budynku o niesymetrycznym rzucie.
Uwagi końcowe
W artykule pokazano obliczenia dla kondygnacji budynku z paneli drewnianych. Sztywności ścian można określić za pomocą elementów powierzchniowych lub prętowych. Uwzględniane są przy tym sprężystości wynikające z zakotwienia ścian w stropach.
W załączonym pliku Excel można odtworzyć obliczenia z przykładów.
Ostatnia część tej serii przedstawia obliczanie sił określonych na podstawie reakcji podporowych na liniach (patrz Rysunek 05).
