La clausola 8.4.1 [1] elenca i requisiti di stabilità che la verifica strutturale dovrebbe affrontare utilizzando entrambi i metodi. Questi includono deformazioni che contribuiscono alla struttura, effetti del secondo ordine tra cui P-Δ e P-δ, imperfezioni geometriche globali e dell'asta, riduzione della rigidezza che tiene conto dello snervamento dell'asta e delle tensioni residue e, infine, incertezza nella rigidezza della struttura e forza.
Clausola 8.4.3 - Metodo di analisi di stabilità semplificato
Con il metodo di analisi di stabilità semplificato fornito in 8.4.3 [1], sono elencati solo un paio di requisiti.
Non linearità geometriche
Il primo include gli effetti del secondo ordine dell'asta, o P-Δ, che possono essere considerati direttamente nell'analisi. Un metodo di calcolo dell'analisi del secondo ordine è più comune con molti programmi software di analisi strutturale oggi. L'alternativa è amplificare tutti i carichi assiali delle aste e i momenti flettenti ottenuti da un'analisi del primo ordine del coefficiente U2 definito in 8.4.3.2(b) [1]. Questo approccio può essere più adatto per i calcoli manuali o se il software di analisi strutturale non include automaticamente gli effetti P-Δ.
Imperfezioni geometriche
I carichi laterali fittizi sono il secondo elemento elencato con il metodo semplificato nella clausola 8.4.3.3 [1]. Questo carico applicato è uguale a 0,005 volte il carico gravitazionale totale fattorizzato al piano considerato e dovrebbe essere distribuito in modo simile al carico gravitazionale. I carichi fittizi sono sempre applicati nella direzione che genera il maggiore effetto destabilizzante. Ciò significa che tali carichi dovrebbero essere applicati nella stessa direzione di un carico del vento laterale per generare le deformazioni più elevate e le forze interne sulla struttura.
Appendice O.2 – Effetti di stabilità nell'analisi elastica
In alternativa all'approccio semplificato dell'analisi di stabilità di cui sopra, gli ingegneri possono utilizzare l'Appendice O.2 per soddisfare i requisiti di stabilità stabiliti nella clausola 8.4.1 [1]. Questo approccio è stato aggiunto alla norma 2019 e ha molte somiglianze con il manuale americano di progettazione acciaio AISC 360-16 cap. C Metodo di analisi diretta.
Non linearità geometriche
Le non linearità geometriche, o effetti del secondo ordine, sono trattate in O.2.2 [1]. Come il metodo semplificato, è possibile eseguire direttamente un'analisi del secondo ordine, che include gli effetti dei carichi agenti nei punti di intersezione spostati delle aste' (effetti P-Δ). Inoltre, dovrebbero essere considerati gli effetti dei carichi assiali che agiscono sulla forma dell'asta inflessa lungo la lunghezza (P-δ). Le disposizioni sono fornite in O.2.2 [1] dove P-δ può essere completamente trascurato. D'altra parte, se P-δ è incluso direttamente nell'analisi, il coefficiente U1 può essere impostato su 1.0 utilizzato nella clausola 13.8 - Verifica di aste di compressione e flessione assiale [1].
Imperfezioni geometriche
Le imperfezioni geometriche dell'asta come l'asta fuori rettilineità o le imperfezioni geometriche locali come l'elemento fuori rettilineità per le aste non devono essere considerate durante la verifica secondo la clausola O.2 [1 ]. Tuttavia, le imperfezioni geometriche globali dovrebbero essere considerate con la modellazione diretta o con l'uso di carichi laterali fittizi. C'è l'eccezione, tuttavia, che queste imperfezioni geometriche globali possono essere trascurate per le combinazioni di carico laterale solo se soddisfano i requisiti stabiliti nella clausola O.2.3.1 [1]. I requisiti includono che i carichi gravitazionali della struttura sono supportati principalmente da elementi strutturali verticali e il rapporto tra lo spostamento massimo del piano del 2° ordine e lo spostamento del piano del 1° ordine utilizzando una rigidezza ridotta dell'asta secondo la clausola O.2.4 [1] non supera 1,7 a qualsiasi livello del piano.
Quando l'ingegnere non può trascurare queste imperfezioni, può essere utilizzato il primo metodo di modellazione diretta. I punti di intersezione delle aste dovrebbero essere spostati dalle loro posizioni originali. L'ampiezza di questo spostamento iniziale è indicata nella clausola 29.3 [1] e applicata nella direzione di massima destabilizzazione, che per la maggior parte delle strutture edilizie è una tolleranza di 1/500 per la colonna fuori-- a piombo. Il problema significativo con questo metodo è l'elevato numero di scenari del modello che devono essere considerati. In teoria, sono necessari quattro spostamenti nelle quattro diverse direzioni a ogni livello del piano. Se gli effetti di fuori rettilineità dell'asta sono anche accoppiati con la colonna fuori piombo, questo aggiunge molti altri scenari di modellazione da considerare per soddisfare il massimo effetto destabilizzante.
Il metodo alternativo e preferito per le imperfezioni geometriche globali è applicare i carichi laterali teorici. Questo metodo è consentito solo quando i carichi gravitazionali sono supportati principalmente da elementi strutturali verticali. I carichi laterali fittizi sono stati trattati in precedenza in questo articolo e sono applicati nello stesso modo dell'analisi di stabilità semplificata nella clausola 8.4.3.2 [1]. Tuttavia, l'ampiezza viene ridotta da 0,005 a 0,002 volte il carico gravitazionale fattorizzato al piano pertinente. La riduzione di grandezza è consentita nella clausola O.2.3.3, poiché questi carichi teorici tengono conto solo delle imperfezioni geometriche globali, mentre i carichi teorici nella clausola 8.4.3.2 [1] tengono conto anche di effetti di inelasticità e altre incertezze.
Effetti di inelasticità
Per tenere conto degli effetti di inelasticità e per considerare anche l'asta iniziale o le imperfezioni geometriche locali, nonché l'incertezza nella rigidezza e nella resistenza, la rigidezza assiale e flessionale ridotta dell'asta secondo le seguenti equazioni nella clausola O.2.4 [1 ] dovrebbe essere applicato alle aste che contribuiscono alla stabilità laterale.
(EA)r = 0.8 τb EA
(EI)r = 0.8 τb EI
Dove,
Cf/Cy < 0,5 ; τb = 1.0
Cf/Cy > 0,5 ; τb = 4
Cf/Cy (1 - Cf/Cy )
Per evitare distorsioni localizzate, la norma suggerisce di applicare questa riduzione di rigidezza a tutte le aste. Inoltre, quando la rigidezza a taglio (GA) e la rigidezza torsionale (GJ) contribuiscono in modo significativo alla stabilità laterale, si dovrebbe considerare la riduzione della rigidezza. La riduzione della rigidezza non deve essere utilizzata durante l'analisi di derive, inflessioni, vibrazioni o vibrazioni naturali.
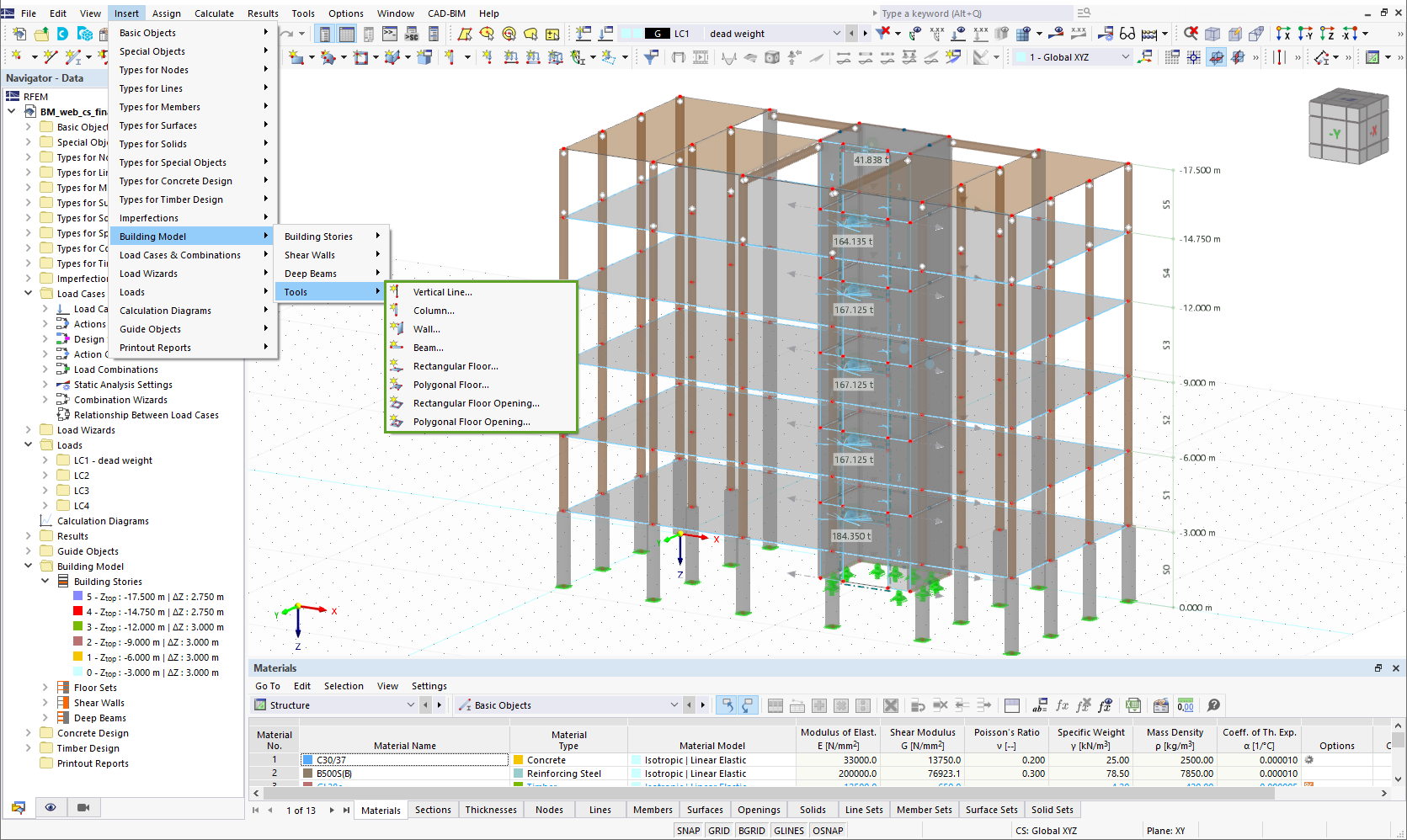
Appendice O.2 Applicazione in RFEM
Il programma FEA RFEM ha incorporato gli ultimi requisiti di stabilità della norma CSA S16:19 secondo le nuove disposizioni dell'Appendice O.2.
Non linearità geometriche
Gli effetti del secondo ordine indicati nella clausola O.2.2 [1] sono considerati direttamente per ogni caso di carico o combinazione di carico quando il metodo di calcolo è impostato su "analisi del secondo ordine".
Non solo gli effetti P-Delta sono inclusi per l'analisi dell'asta, ma sono anche considerati P-δ. Pertanto, il coefficiente U1 può essere impostato su 1.0 specificato nella clausola 13.8 direttamente nel modulo di verifica dell'asta RF-/STEEL CSA.
Imperfezioni geometriche
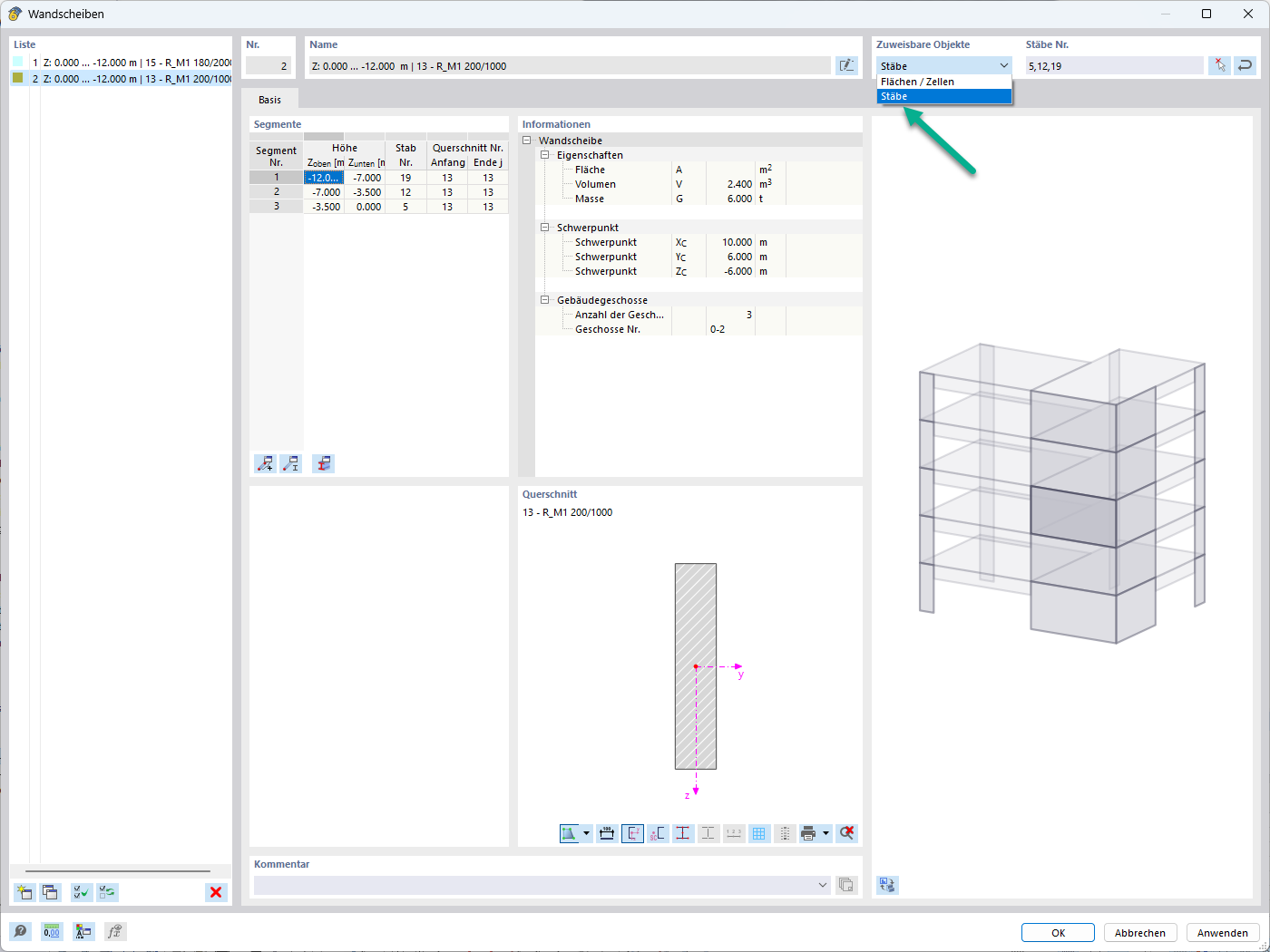
L'utente di RFEM ha la possibilità di modellare direttamente le imperfezioni geometriche globali spostando i punti o i nodi delle intersezioni delle aste. Tuttavia, per garantire che questo metodo crei il massimo effetto destabilizzante, sarà necessario eseguire più modelli con vari scenari. Questo è piuttosto lungo e ingombrante.
L'approccio alternativo consiste nell'applicare i carichi nozionali con le opzioni di imperfezione all'interno di RFEM. Questa finestra di dialogo ora include CSA S16:19 nelle opzioni a discesa. Il carico teorico viene applicato all'estremità dell'asta (cioè alla sommità della colonna) con una grandezza uguale a 0,002 (o 0,005 se si utilizza il metodo di stabilità semplificato) moltiplicata per la forza assiale dell'asta's (carico di gravità dell'asta applicato). Una forza uguale e opposta viene applicata internamente all'estremità opposta dell'asta per evitare il taglio non realistico della base della struttura.
Questi casi di carico di imperfezione possono essere applicati in RFEM con casi di carico laterali specifici per produrre la massima azione destabilizzante evitando la generazione di combinazioni di carico che non saranno controllanti e aumenteranno ulteriormente il tempo di calcolo (ovvero, i carichi teorici nella direzione X dovrebbero essere applicato solo con carichi del vento in direzione X). Inoltre, le imperfezioni possono essere disattivate completamente per le espressioni di combinazioni di carico come lo stato limite di esercizio mentre sono ancora applicate alle combinazioni di resistenza.
Effetti di inelasticità
La scheda Modifica rigidezza per le aste ora include la norma CSA S16:19. Quando questa opzione è selezionata, il coefficiente di modifica 0.8 e il coefficiente τb calcolato vengono applicati direttamente alla rigidezza flessionale e assiale dell'asta. Gli utenti hanno anche la possibilità di applicare ulteriormente queste riduzioni alla rigidezza torsionale e a taglio dell'asta.
Poiché la riduzione della rigidezza dell'asta non dovrebbe essere considerata per la verifica dello stato limite di esercizio (cioè le inflessioni), RFEM consente agli utenti di disattivare tutte le modifiche di rigidezza dell'asta per le combinazioni di carico di esercizio lasciandolo attivo per le combinazioni di carico di resistenza.
Sommario
Gli aggiornamenti significativi della verifica di stabilità secondo l'Appendice O.2 nell'ultimo manuale canadese di verifica acciaio CSA S16:19 sono ora completamente incorporati nel flusso di lavoro di analisi di RFEM. Questi aggiornamenti includono in modo più significativo la capacità di considerare i carichi nozionali come imperfezioni, nonché le rigidezze ridotte delle aste secondo CSA S16:19. Per vedere questi nuovi aggiornamenti mostrati in un video di esempio dettagliato, dai un'occhiata al webinar CSA S16:19 Steel Design in RFEM.














..png?mw=320&hash=bd2e7071b02d74aef6228d22c4b83867d2d7e1a5)






































-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)