Verifikační příklady

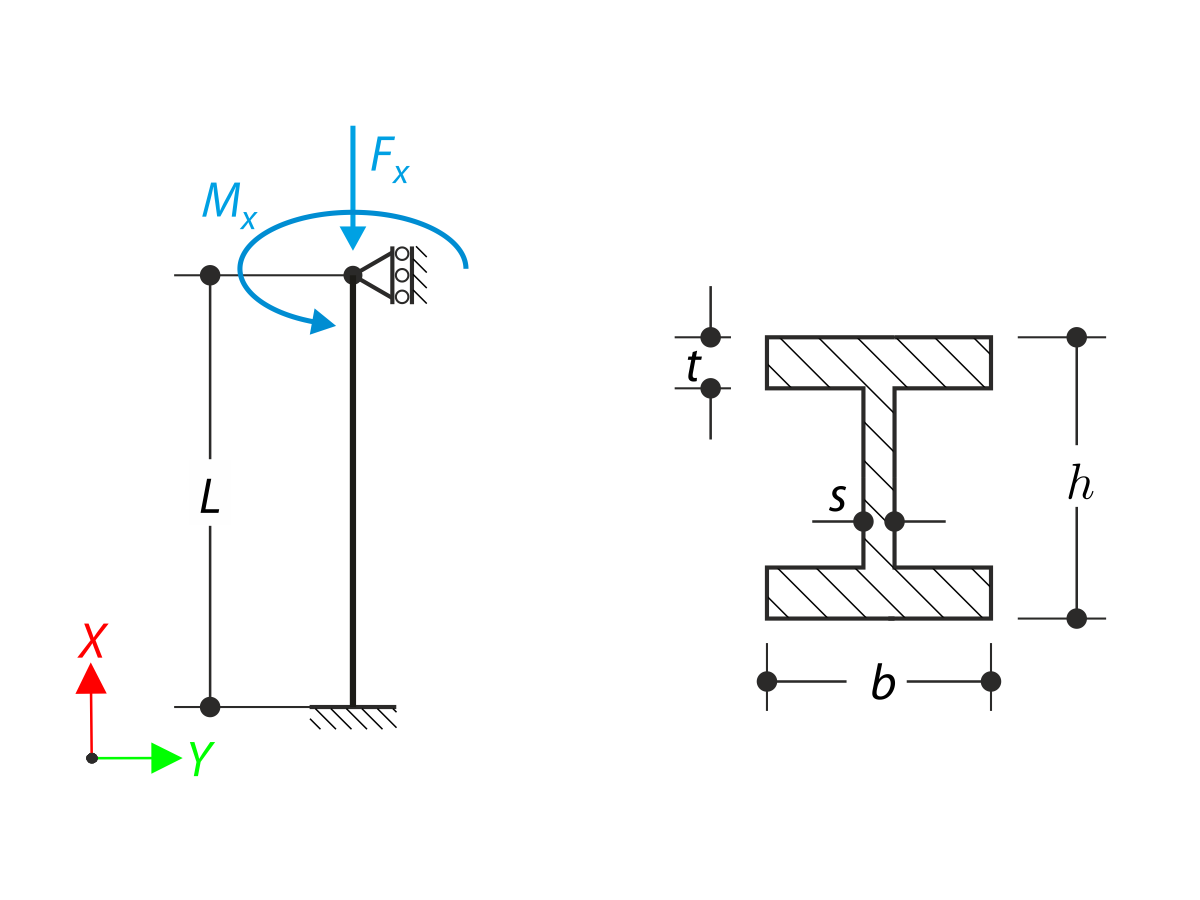
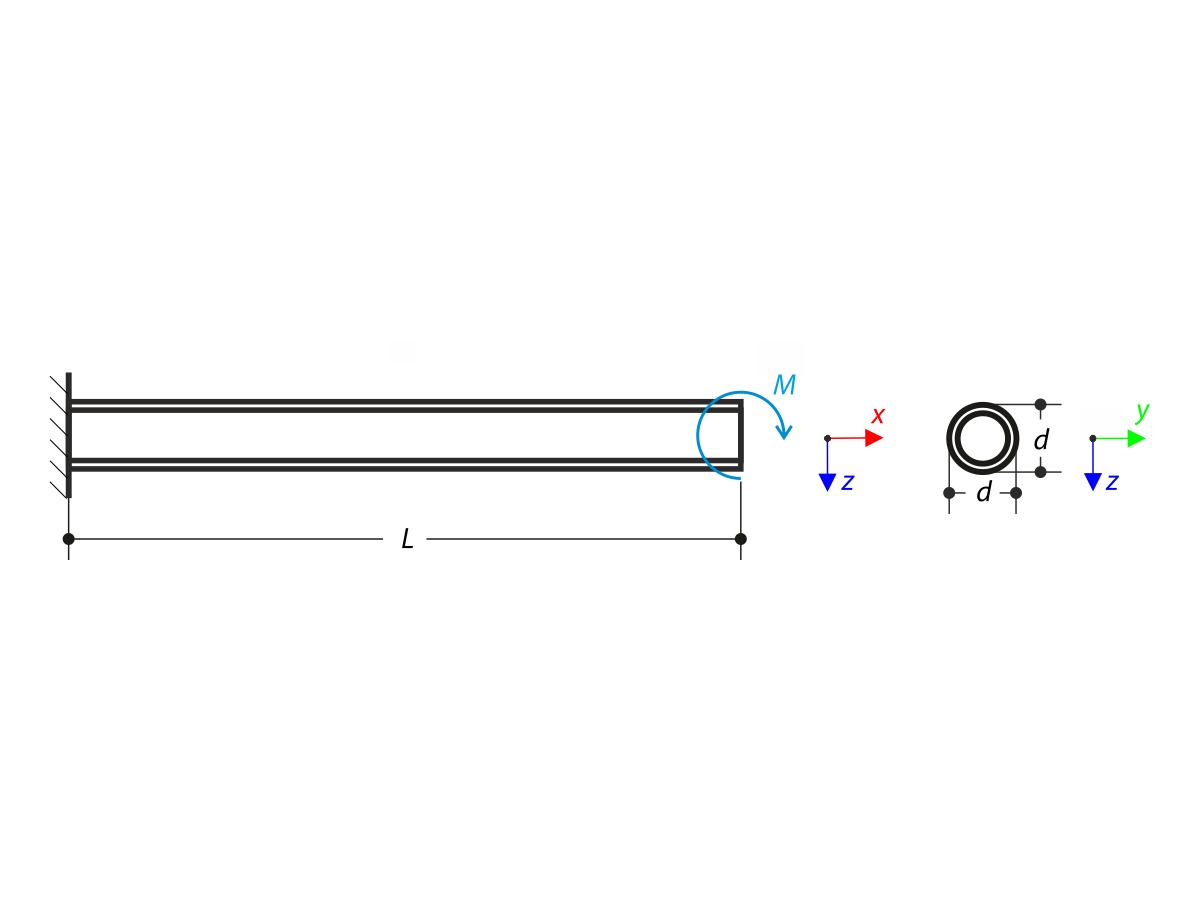
Tenká deska je upevněna na jedné straně (φ_z = 0) a na druhé straně je zatížena rovnoměrným momentem. Nejdříve modelujeme desku jako rovinnou plochu. Kromě toho je deska modelována jako čtvrtina válcové plochy. Šířka rovinného modelu se rovná délce jedné čtvrtiny kružnice zakřiveného modelu. Zakřivený model tak má téměř stejnou torzní konstantu J jako rovinný model. Stanovte maximální pootočení desky φ_z,max pro oba geometrické modely a porovnejte výsledky pomocí Kichhoffovy a Mindlinovy teorie desek.

Validace ve větrném inženýrství je rozhodující pro zajištění konstrukční integrity antén proti silám způsobeným větrem. Ve spolupráci s RWTH University v Cáchách vědci kombinují testování ve větrném tunelu a simulace, aby zdokonalili modely a zvýšili přesnost. Tato studie zlepšuje odolnost antén, což přináší výhody odvětvím závislým na konstrukcích vystavených působení větru.

Tento příklad vychází ze zkoušky mezní vrstvy atmosféry (ABL) z dokumentu německého WTG: Informační list pro výbor 3 - Numerická simulace proudění větru, kapitola 9.1 (viz odkazy). Před každou numerickou simulací je třeba zkontrolovat, zda mezní vrstva atmosféry definovaná na přítoku zasahuje do konstrukce, a to testováním jejího vývoje v prázdném tunelu. To ovlivňuje nejen průběh rychlostí, ale také turbulentní veličiny. Zkouška musí být provedena pro stacionární (RANS) i nestacionární (URANS, LES) výpočty. V následujícím příspěvku předvedeme vývoj rychlostního pole, pole kinetické energie turbulence a pole rychlosti disipace turbulence pro čtyři kategorie terénu I až IV definované v EN 1991-1-4. Svislá anizotropní turbulence podle podle kapitoly 6.3.1 a RANS k-ω turbulentního modelu.

Konzola z materiálu s různou plastickou pevností v tahu a v tlaku je plně fixována na levém konci a zatížena ohybovým momentem podle následujícího náčrtu. Problém je popsán pomocí následující sady parametrů. V tomto příkladu se zohlední malé deformace a vlastní tíha se zanedbá. Stanovíme maximální průhyb u_z,max.

Stanovte požadované pevnosti a součinitele vzpěrné délky pro sloupy podle ASTM A992 v momentovém rámu znázorněném na obrázku 1 pro maximální kombinaci tíhového zatížení pomocí LRFD a ASD.

Prut s W-profilem podle ASTM A992 je vybrán tak, aby unesl vlastní tíhu 30 000 kips a užitné zatížení 90 000 kips v tahu. Ověřte pevnost prutu pomocí LRFD a ASD.

Sloup s profilem ASTM A992 14×132 W je zatížen danými osovými tlakovými silami. Sloup je nahoře i dole rotačně uložen. Na základě LRFD a ASD určíme, zda je sloup adekvátní pro přenos zatížení znázorněném na obrázku 1.

Uvažujme prostý nosníku ASTM A992 W 18x50 s vlastní tíhou a spojitým užitným zatížením, jak je znázorněno na obrázku 1. Maximální jmenovitá výška prutu je 18 palců. Průhyb při užitném zatížení je omezen na L/360. Nosník je prostě podepřen a spojitě ztužen. Ověřte dostupnou pevnost v ohybu vybraného nosníku na základě LRFD a ASD.

Na obrázku 1 je znázorněn nosník ASTM A992 W 24×62 se smykem na konci 48 000 a 145 000 kips od vlastní tíhy a užitného zatížení. Ověřte dostupnou smykovou únosnost vybraného nosníku na základě LRFD a ASD.

Pomocí tabulek v manuálu AISC zjistěte dostupné pevnosti v tlaku a ohybu a zjistěte, zda má nosník ASTM A992 W14x99 dostatečnou únosnost pro nesení normálových sil a momentů znázorněných na obrázku 1, které byly získány z analýzy druhého řádu, která zahrnuje P-𝛿 účinky.

Tento verifikační příklad je modifikací VE0064 - Silnostěnná nádoba, kde je rozdíl že materiál nádoby je nestlačitelný. A thick-walled vessel is loaded by inner and outer pressure. The vessel is open-ended, thus there is no axial stress. The problem is modeled as a quarter model and described by the following set of parameters. While neglecting self-weight, determine the radial deflection of the inner and outer radius u_r(r₁), u_r(r₂).

Silnostěnná nádoba je zatížena vnitřním tlakem, který se volí tak, aby nádoba dosáhla pružno-plastického stavu. Příklad je modelován jako čtvrtinový model. Stanovte a porovnejte analytické a numerické řešení radiální polohy hranice plastické oblasti r_y podle Trescovy hypotézy pro plochu plasticity bez zanedbání vlastní tíhy.

Dvouvrstvá silnostěnná nádoba je zatížena vnitřním a vnějším tlakem. Nádoba je otevřená, a proto nevzniká žádné osové napětí. Příklad je modelován jako čtvrtinový model. Stanoví se radiální průhyb vnitřního a vnějšího poloměru u_r (r₁ ), u_r (r₂ ) a tlak (radiální napětí) ve středním poloměru p_m. Vlastní tíhu zanedbáme.

Silnostěnná nádoba je zatížena vnitřním a vnějším tlakem. Nádoba je otevřená, a proto nevzniká žádné osové napětí. Příklad je modelován jako čtvrtinový model. Stanoví se radiální průhyb vnitřního a vnějšího poloměru u_r (r₁ ), u_r (r₂ ). Vlastní tíhu zanedbáme.

Kompaktní disk (CD) se otáčí rychlostí 10 000 ot./min. Je tak vystaven odstředivé síle. Příklad je modelován jako čtvrtinový model. Stanoví se tangenciální napětí σ_t na vnitřním a vnějším průměru a radiální průhyb u_r vnějšího poloměru.

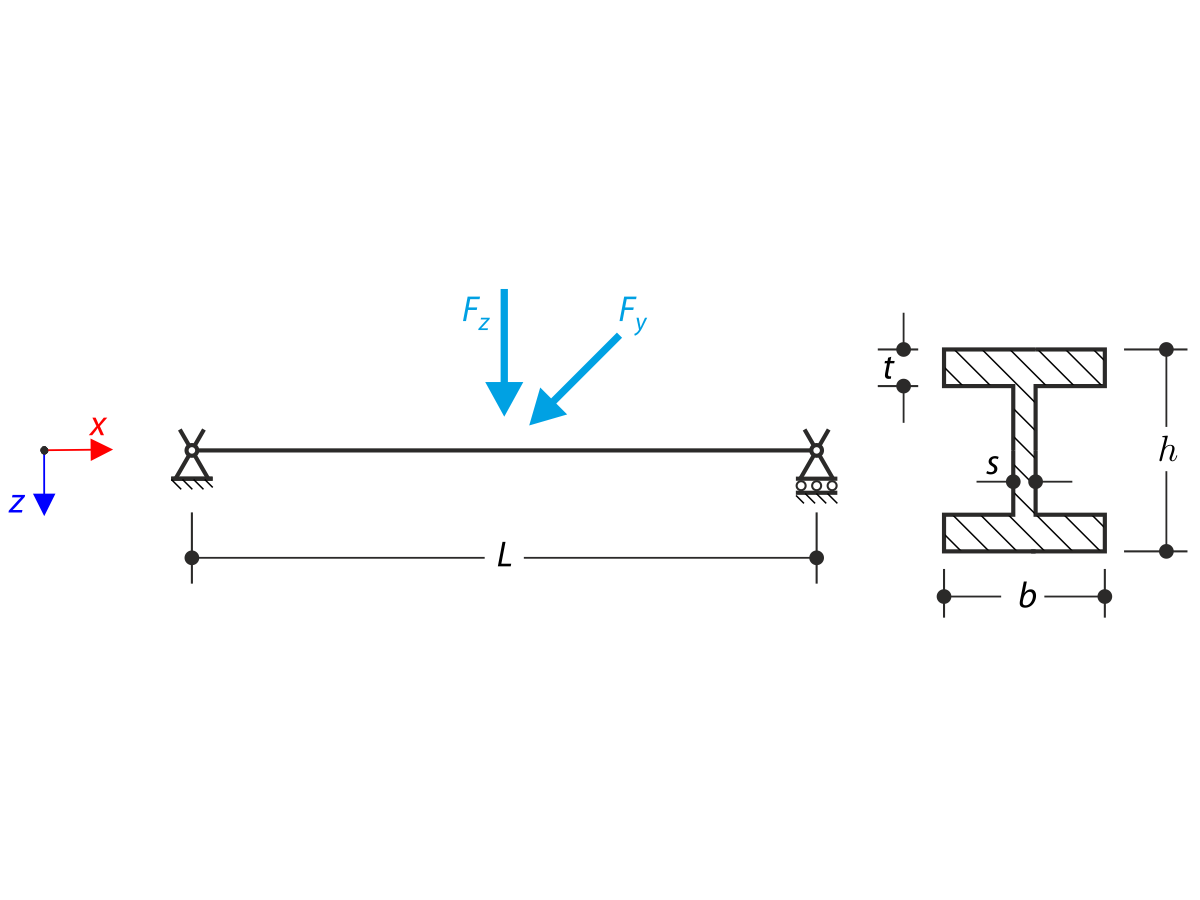
Konstrukce se skládá z prostého nosníku s I-profilem. Osové pootočení φ_x je na obou koncích omezeno, průřez je však bez možnosti deplanace (vidlicová podpora). Nosník má počáteční imperfekci ve směru Y definovanou jako parabolickou křivku s maximálním posunem 30 mm uprostřed. Uprostřed horní pásnice I-profilu působí rovnoměrné zatížení. Problém je popsán pomocí následující sady parametrů. Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.

Konstrukce se skládá z I-profilu a dvou trubkových nosníků. The structure contains several imperfections and it is loaded by the force F_z. Vlastní tíha se v tomto příkladu nezohledňuje. Determine the deflections u_y and u_z and axial rotation φ_x at the endpoint (Point 4). Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.

In this verification example the punching shear resistance of an inner column of a flat slab is examined. The column has a circular secton with a 30cm diameter.

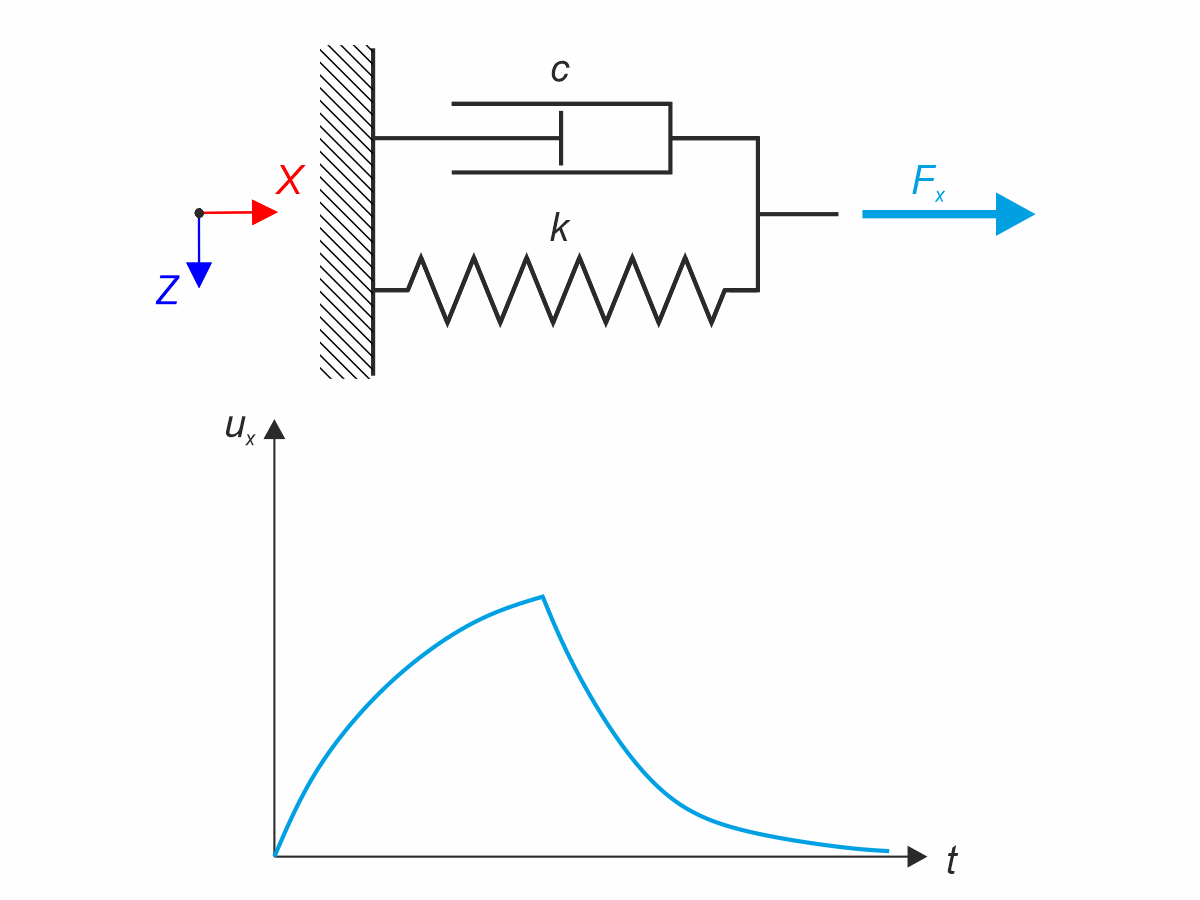
Kelvin-Voigtův materiálový model se skládá z paralelně zapojené lineární pružiny a viskózního tlumiče. V tomto verifikačním příkladu je testováno časové chování tohoto modelu při zatížení a relaxaci v časovém intervalu 24 hodin. Konstantní síla F_x působí po dobu 12 hodin a zbývajících 12 hodin je materiálový model bez zatížení (relaxace). Vyhodnocuje se deformace po 12 a 20 hodinách. Je použita časová analýza s lineární implicitní Newmarkovou metodou.

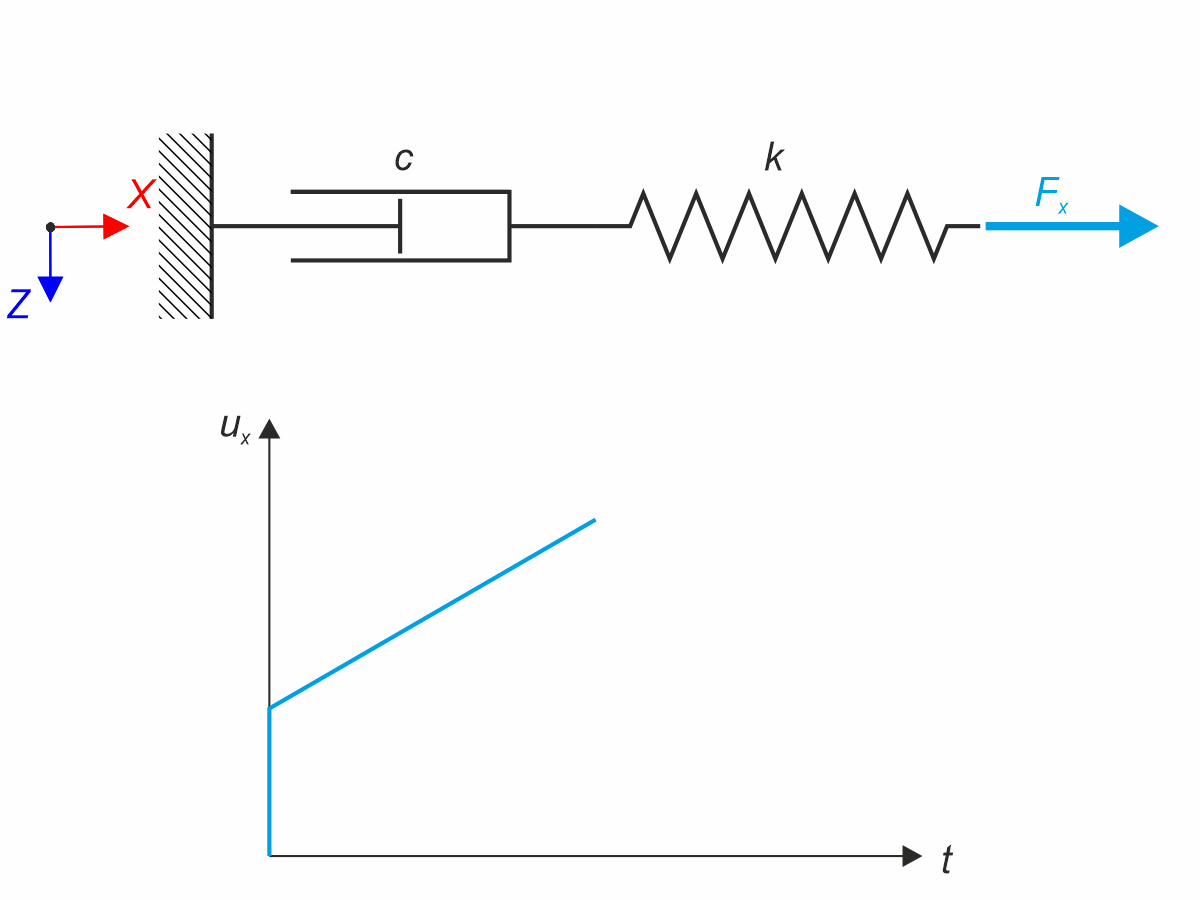
Materiálový model Maxwell se skládá z lineární pružiny a viskózního tlumiče zapojených v sérii. V tomto verifikačním příkladu je testováno časové chování tohoto modelu. Materiálový model podle Maxwella je zatížen konstantní silou F_x. Tato síla způsobuje počáteční deformaci díky pružině, která pak vlivem tlumiče v čase roste. Deformace se sleduje v době zatížení (20 s) a na konci analýzy (120 s). Je použita časová analýza s lineární implicitní Newmarkovou metodou.

Ein Kehlbalken Dach mit gewählter Geometrie wird in Hinblick auf seine Schnittgrößen zwischen Berechnung mittels RFEM 6 und der Handrechnung verglichen. Pokud se týká návrhu 3 Poslední systém pod kontrolou.

Spojitý nosník o čtyřech polích je zatížen normálovými a ohybovými silami (nahrazujícími imperfekce). Všechny podpory jsou vidlicové - deplanace je volná. Stanoví se posuny u_y a u_z, momenty M_y, M_z, M_ω a M_Tpri a natočení φ_x. Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.

V tomto příkladu porovnáváme vzpěrné délky a součinitel kritického zatížení, které lze vypočítat v programu RFEM 6 pomocí addonu Stabilita konstrukce, s ručním výpočtem. Konstrukční systém je tuhý rám se dvěma přídavnými kloubovými sloupy. Tento sloup je zatížen svislými osamělými zatíženími.

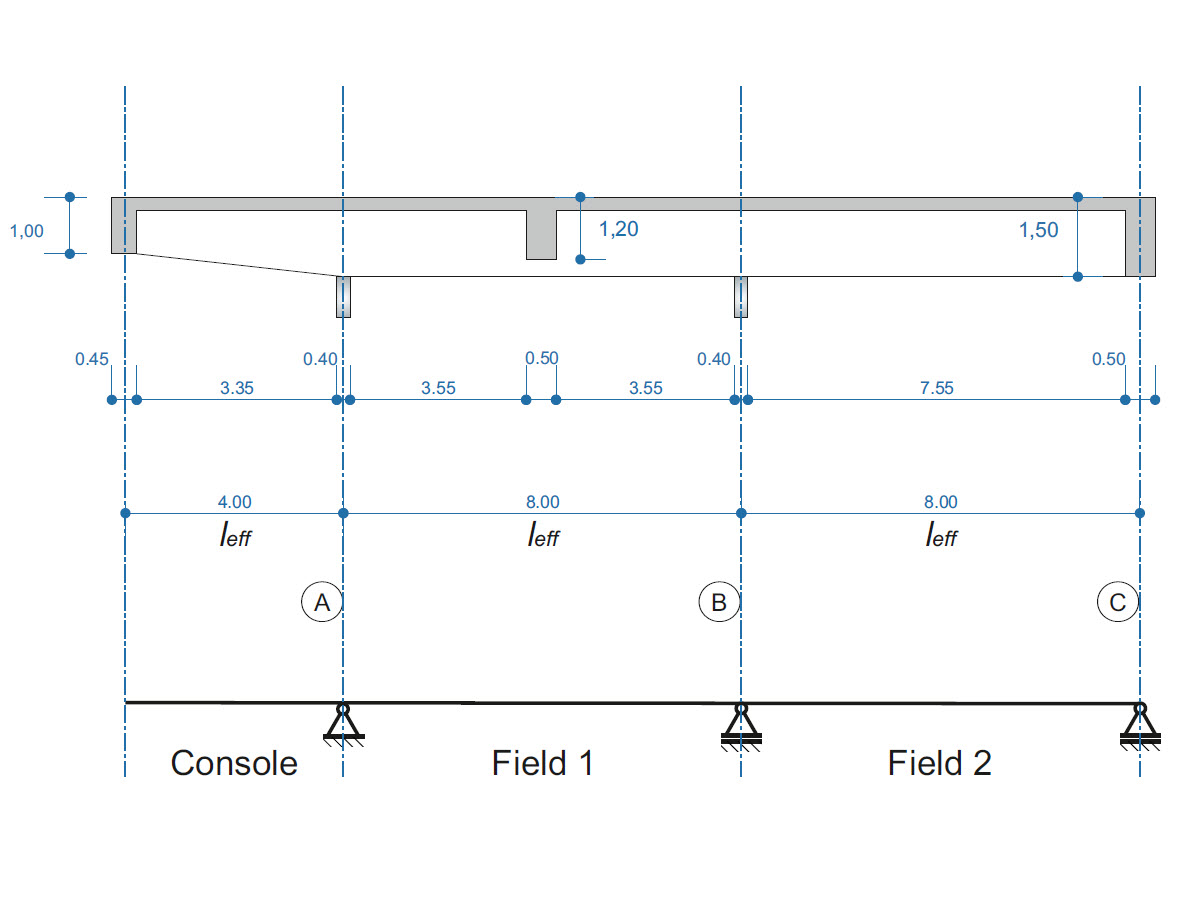
Železobetonový nosník je navržen jako nosník o dvou polích s konzolou. Průřez se mění po délce konzoly (průřez s náběhem). Spočítají se vnitřní síly, nutná podélná a smyková výztuž pro mezní stav únosnosti.

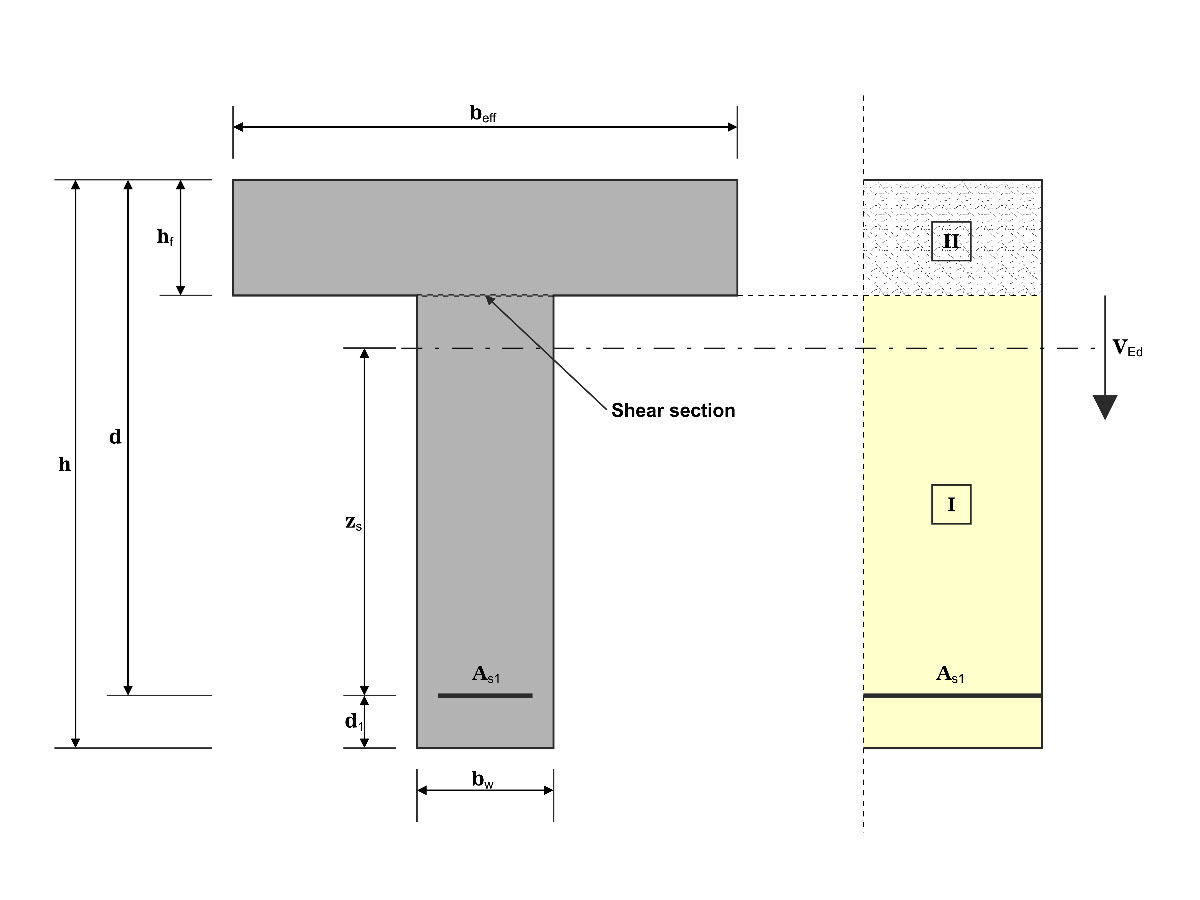
V tomto příkladu se smyk na rozhraní mezi betonem litým v různých okamžicích a příslušnou výztuží stanoví podle DIN EN 1992-1-1. Výsledky získané v programu RFEM 6 budou porovnány s následujícím ručním výpočtem.

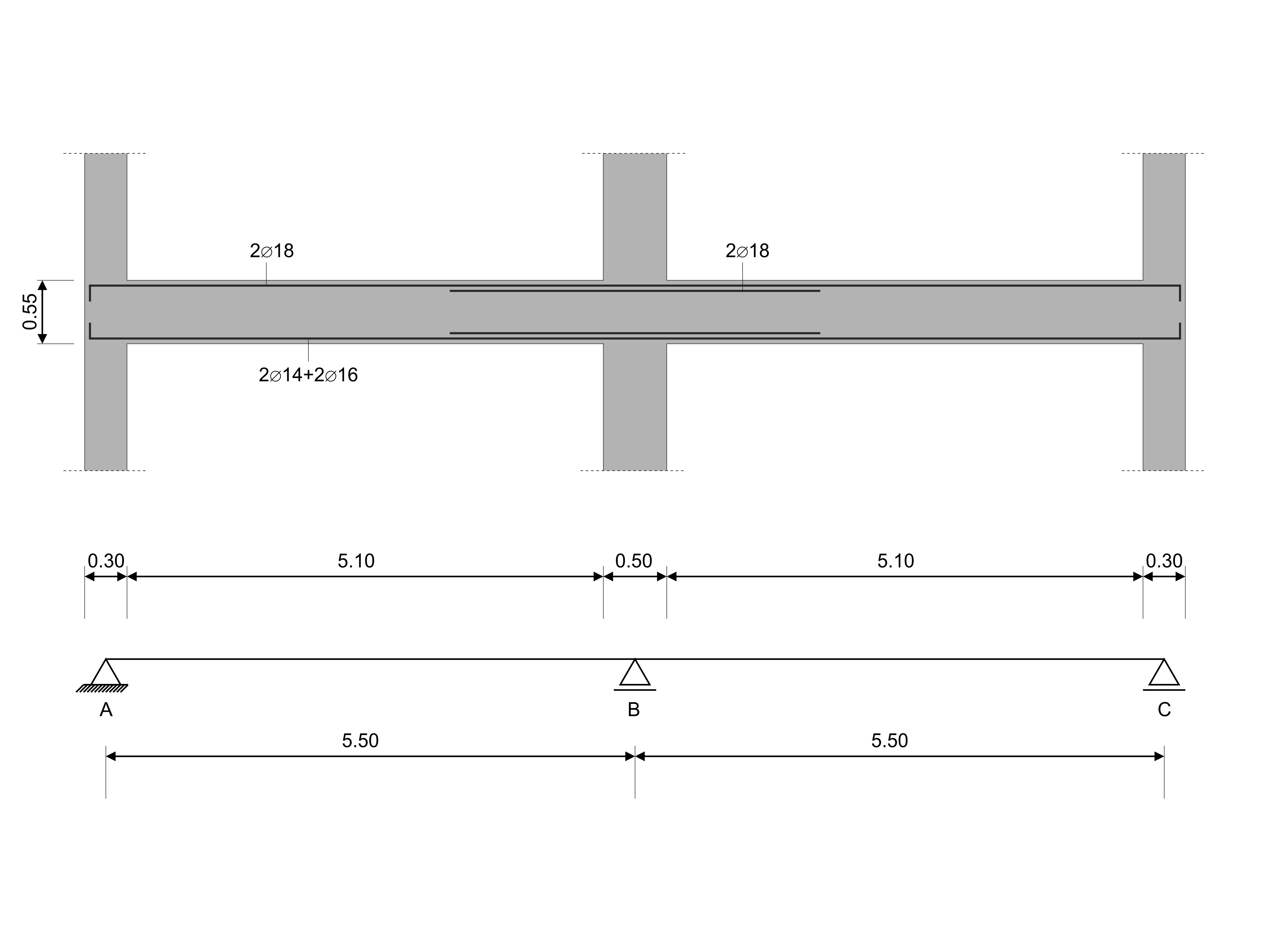
V tomto verifikačním příkladu se vypočítají návrhové hodnoty smykových sil na nosnících podle EN 1998-1, 5.4.2.2 a 5.5.2.1 a také návrhové hodnoty únosnosti sloupů v ohybu podle 5.2.3.3(2). ). Systém tvoří železobetonový nosník o dvou polích s rozpětím 5,50 m. Nosník je součástí rámového systému. Získané výsledky se porovnají s výsledky v [1].

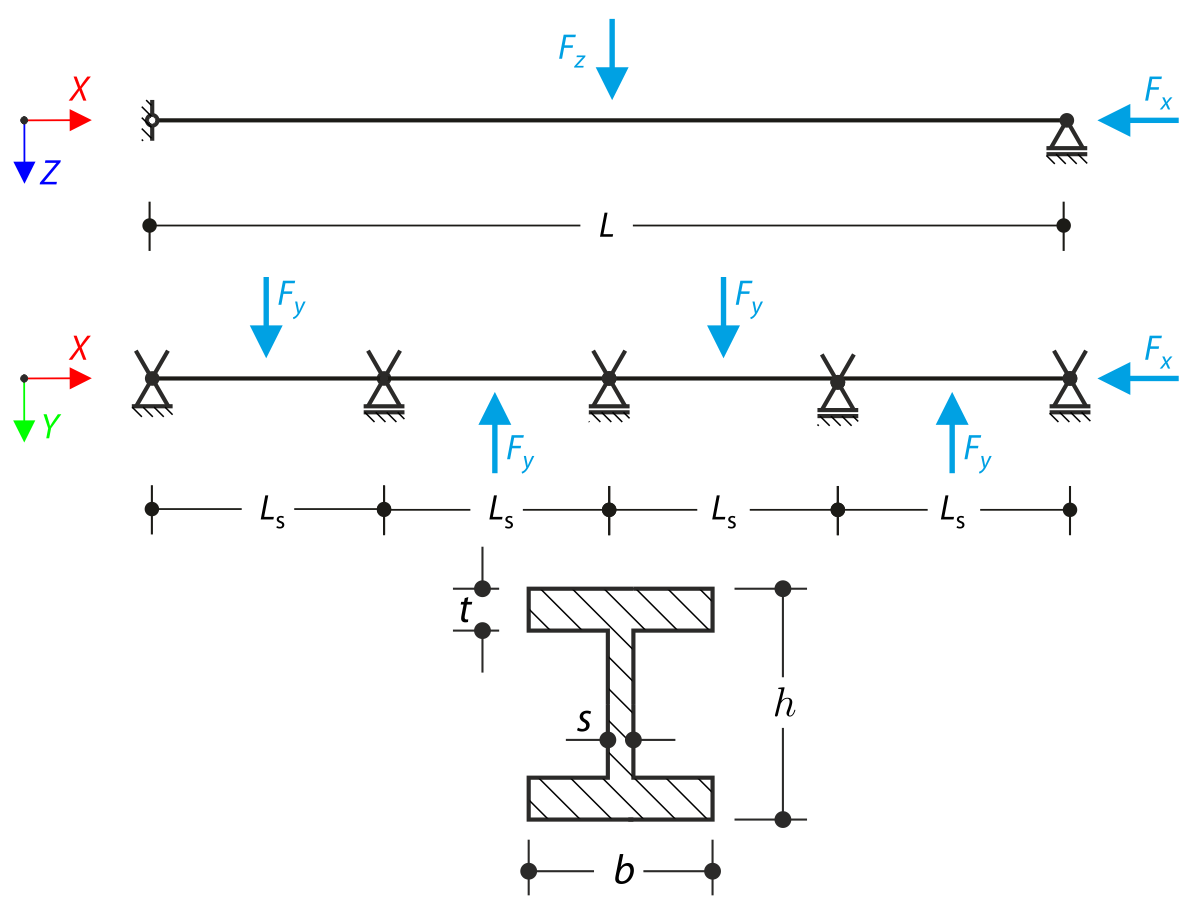
Osové natočení I-profilu je na obou koncích omezeno vidlicovými podpěrami (deplanace není omezena). Konstrukce je zatížena dvěma příčnými silami uprostřed. Vlastní tíha se v tomto příkladu nezohledňuje. Stanoví se maximální průhyby konstrukce u_y,max a u_z,max, maximální natočení φ_x,max, maximální ohybové momenty M_y,max a M_z,max a maximální krouticí momenty M_T,max, M_Tpri,max, M_Tsec,max a M_ω,max. Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.

Prut s danými okrajovými podmínkami je zatížen krouticím momentem a normálovou silou. Při zanedbání vlastní tíhy se stanoví maximální torzní deformace nosníku a jeho vnitřní torzní moment, který je definován jako součet primárního krouticího momentu a krouticího momentu vyvolaného normálovou silou. Tyto hodnoty porovnáme při zohlednění nebo zanedbání vlivu normálové síly. Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.

Konzola je na svém volném konci zatížena momentem. Pomocí geometricky lineární analýzy a analýzy velkých deformací se zanedbáním vlastní tíhy nosníku stanovíme maximální průhyby na volném konci. Verifikační příklad vychází z příkladu, který představili Gensichen a Lumpe.