Vzhledem k geometrickému tvaru a výrobnímu procesu zakřiveného lepeného lamelového dřeva je nutné při posouzení provést samostatnou kontrolu. Zaprvé, průběh ohybového napětí podél výšky nosníku není lineární; Kromě toho vznikají při výrobě napětí v důsledku ohybu lamel. První z nich je způsoben tím, že zrna na vnitřní straně jsou kratší než zrna na vnější straně. Platí tedy následující, za předpokladu Bernoulliho předpokladů (ploché průřezy zůstávají ploché) a za předpokladu, že nulová linie leží v těžišti:
Při zohlednění Hookova zákona jsou vnitřní napětí na okrajích větší než vnější:
fb = E ∙ ε → fb, i > fb, o
Tyto charakteristiky se zohlední při posouzení podle [1] součinitelem zakřivení Cc , který slouží jako součinitel úpravy pro návrhovou hodnotu pevnosti v ohybu:
Fb '= Fb ∙ CD ∙ CM ∙ Ct ∙ CV ∙ Cc
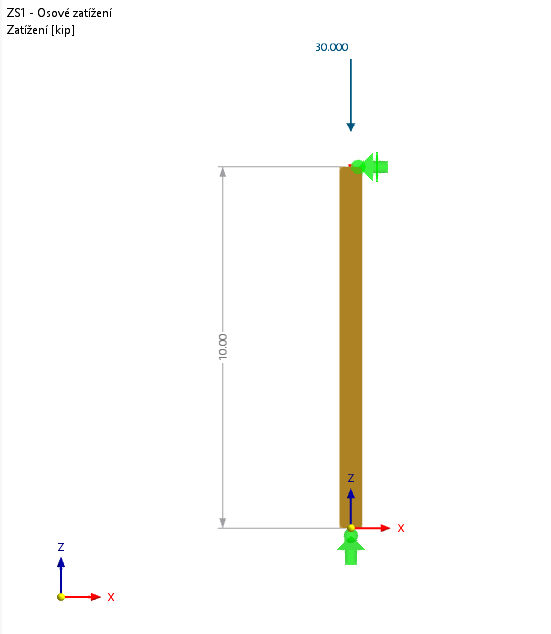
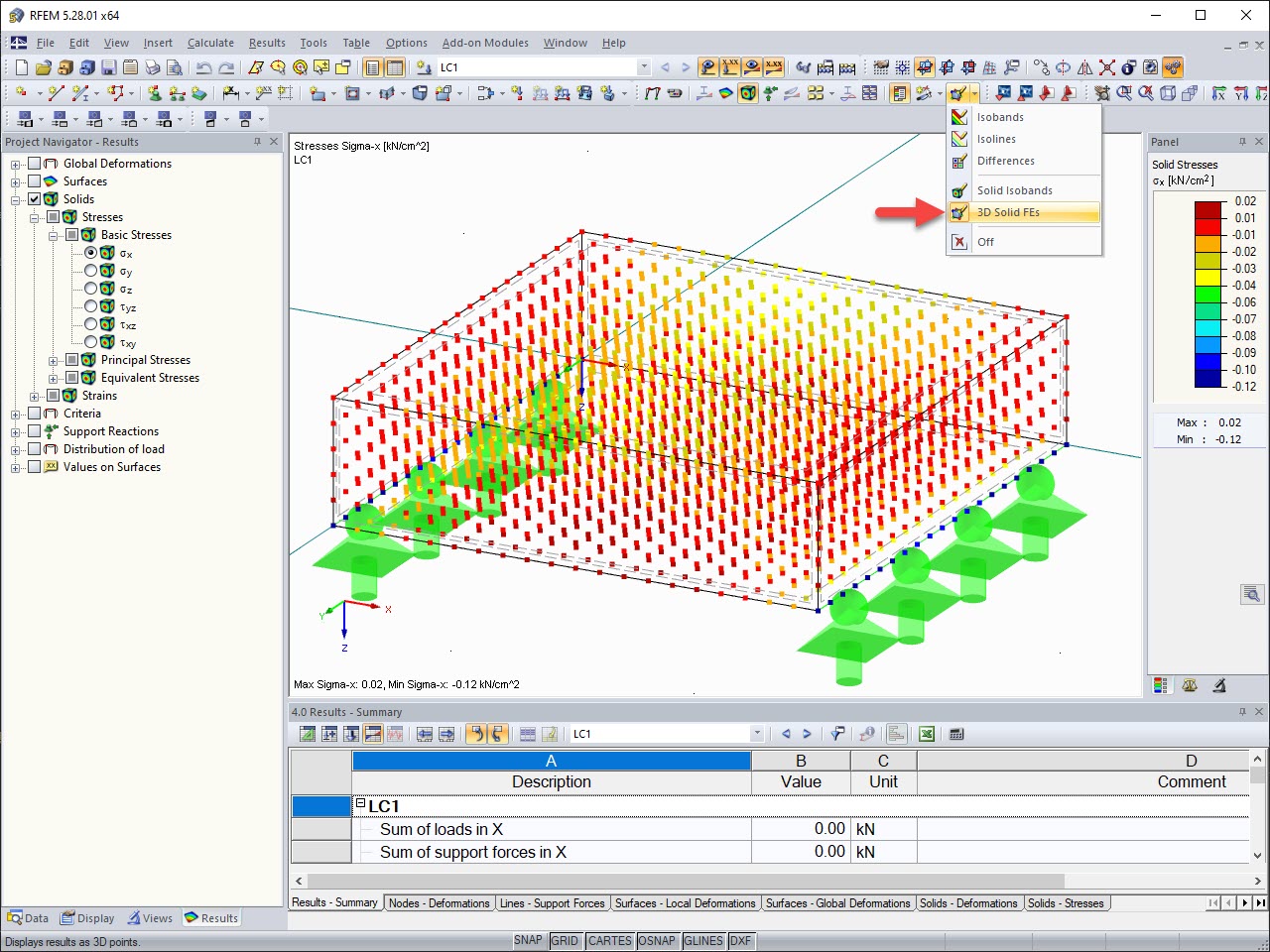
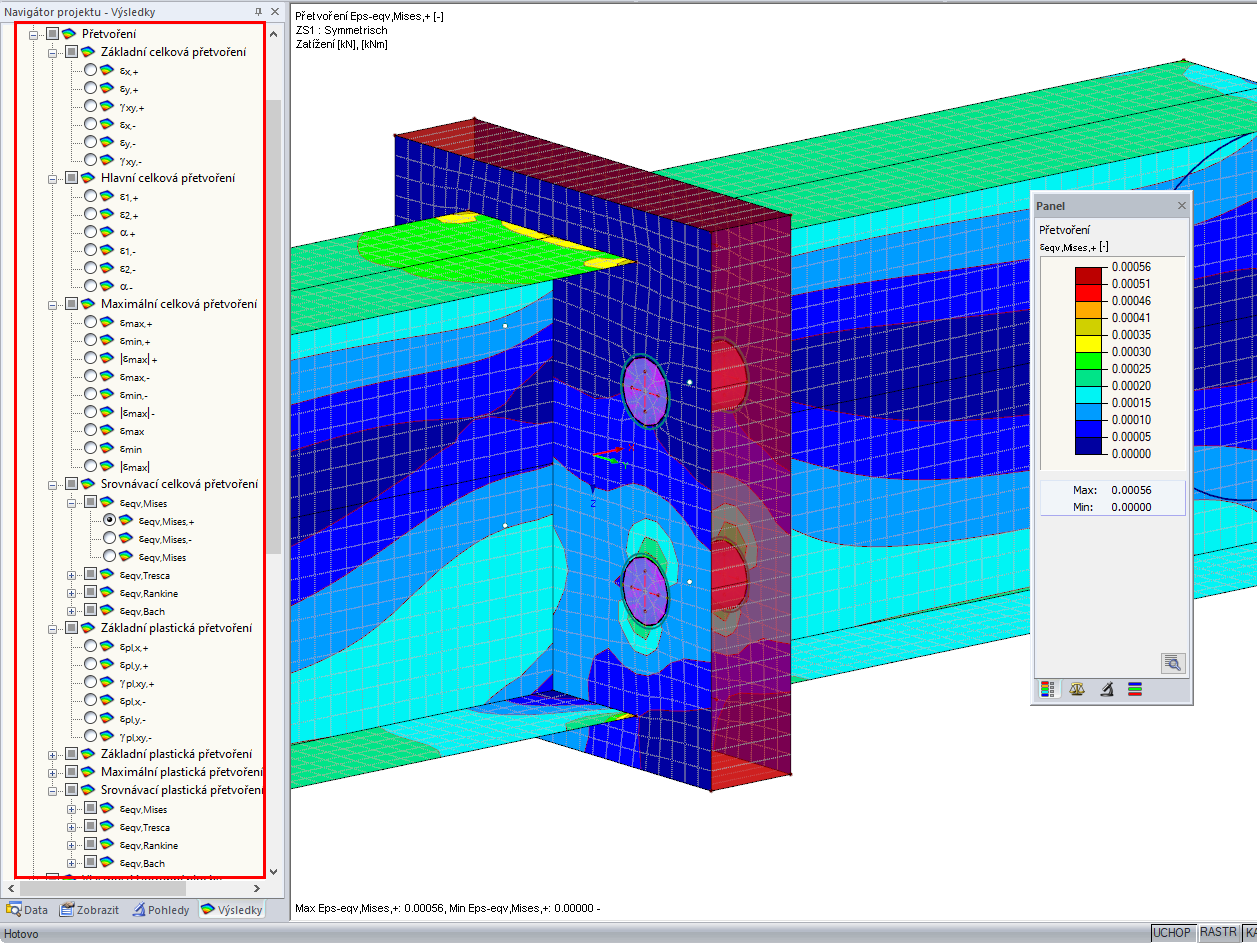
Für das in Bild 03 dargestellte System resultiert unter Berücksichtigung des 20-fachen Eigengewichtes und einer linearen Spannungsverteilung eine maximale Biegespannung im Firstquerschnitt von 1925,1 psi. Betrachtet man die Spannungen in einer FEM-Analyse (siehe Bild 03 unten) werden wegen vorstehender Erläuterung wie erwartet größere Biegespannungen (1986,4 psi) ausgegeben.
Při posouzení zakřivených nosníků v modulu RF-/TIMBER AWC sezohledňuje tento nesoulad s součinitelem zakřivení C c , jak je požadováno v [1] (viz Obrázek 04).
Vergrößert das Biegemoment den Krümmungsradius, entstehen dadurch zusätzlich Zugspannungen quer zur Faser. Pokud ohybový moment zmenší poloměr zakřivení, vznikají na vláknech tlaková napětí. Schematické znázornění toho, jak k těmto napětím dochází, je znázorněno na obr. 05, přičemž se zohledňuje lineární průběh podélného napětí (fb, x ).
Tato radiální napětí je třeba při posouzení zohlednit, protože mají rozhodující vliv na únosnost. Výsledkem je konstantní průřez přes hloubku nosníku:
Ve výšce neutrální osy se napětí stanou maximálními, z čehož vyplývá:
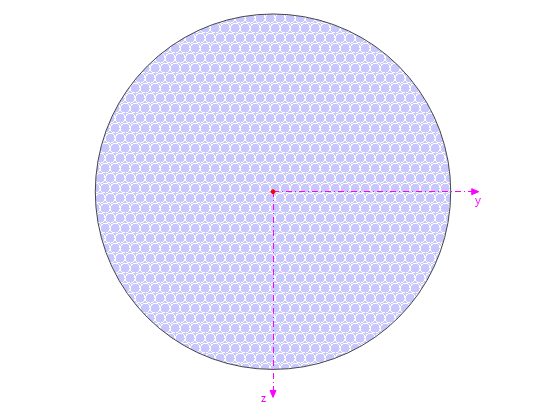
Protože tato radiální napětí nelze určit pomocí nosníku (1D), je třeba je stanovit analyticky. Na obr. 06 jsou znázorněny výsledky z MKP (2D) pro příčné (nahoře) a příčné (dole). Výsledky jsou téměř totožné s analytickým řešením použitým pro posouzení nosníku v modulu RF-/TIMBER AWC (viz obr. 07).
Pokud kontrola není k dispozici, praskne dřevo v úrovni neutrální osy (viz obr. 05 vpravo). Aby se tomu předešlo, je možné zašroubovat příčné tahové výztuže, například ve formě šroubů s plným závitem, které přenášejí příčná tahová napětí. Sílu působící na šroub lze určit přibližně ručně následujícím způsobem:
Tr,t = frt ∙ b ∙ s = 35,4 psi ∙ 8,75 in ∙ 11,5 in = 3,562 lbf
Tr, t = radiální síla ve šroubu
frt = radiální tahové napětí
b = šířka nosníku
s = vzdálenost mezi radiální výztuží
V případě plošného modelu v programu RFEM lze tyto síly integrovat přímo z vnitřních sil v plochách na výsledkový prut. Tento výsledkový prut nepřináší do systému žádnou další tuhost, ale integruje pouze vnitřní síly v plochách. Lze tak přímo odečíst normálovou sílu nosníku nebo výztužného prvku (viz obr. 08).
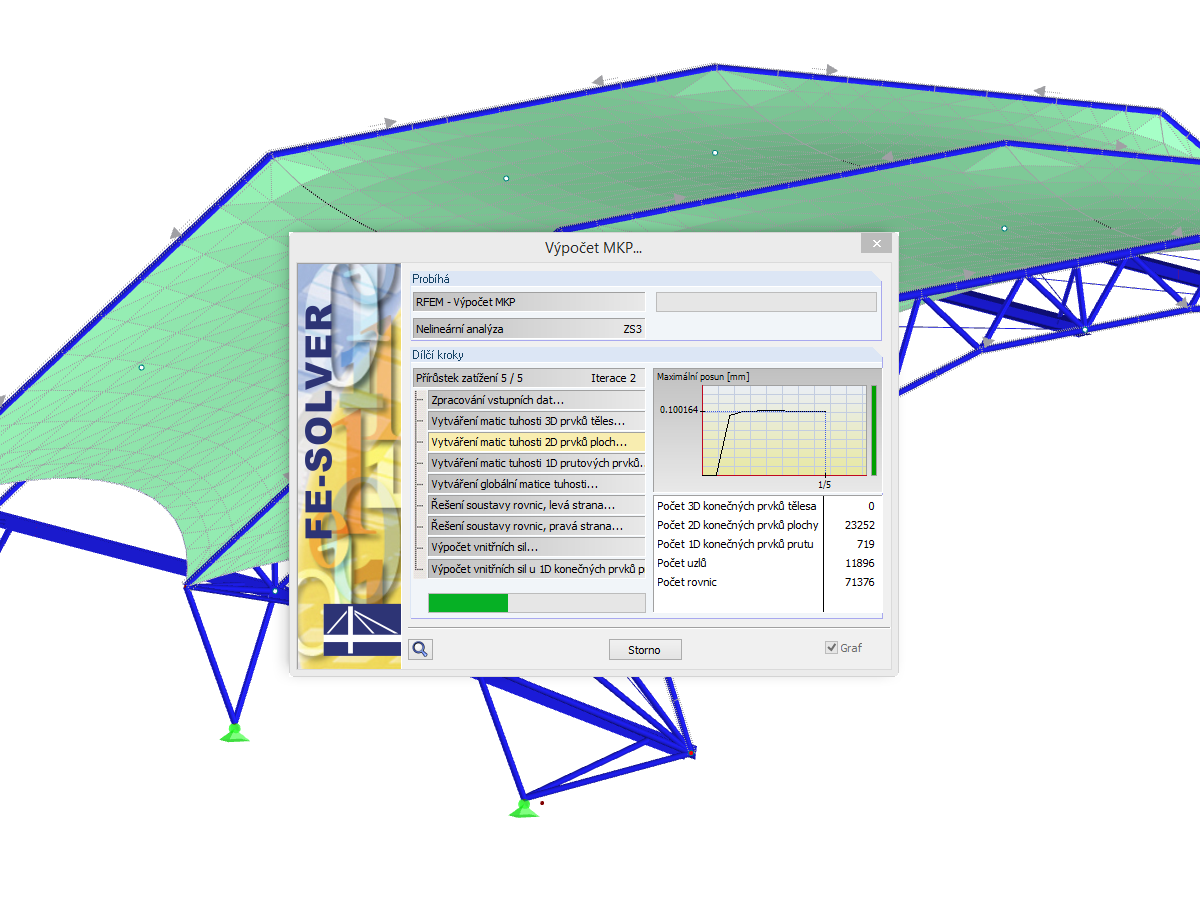
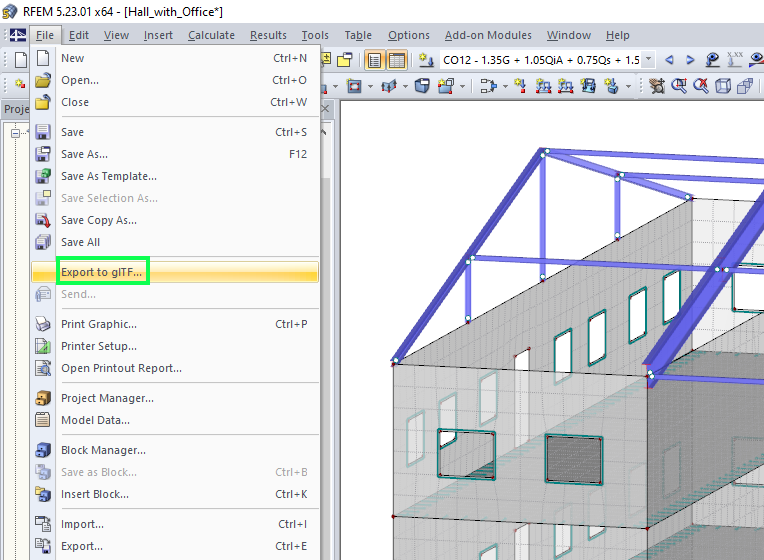
V programu RFEM lze detailně navrhnout i složitější formy podpory. Pokud se tvary nosníků liší od normovaných tvarů nosníků, může být užitečný výpočet metodou konečných prvků s plochami, jak je popsáno výše.