Le calcul de la déformation utilisé s'appuie sur le premier article de cette série.
Rigidité d'un mur
La rigidité d'un mur est calculée avec application d'une charge unitaire de 1 kN. Pour plus d'informations sur les équations utilisées ici, nous vous invitons à consulter l'ouvrage [1] de la section Littérature au bas de cet article et l'article de notre base de connaissance mentionné précédemment.
Exemple
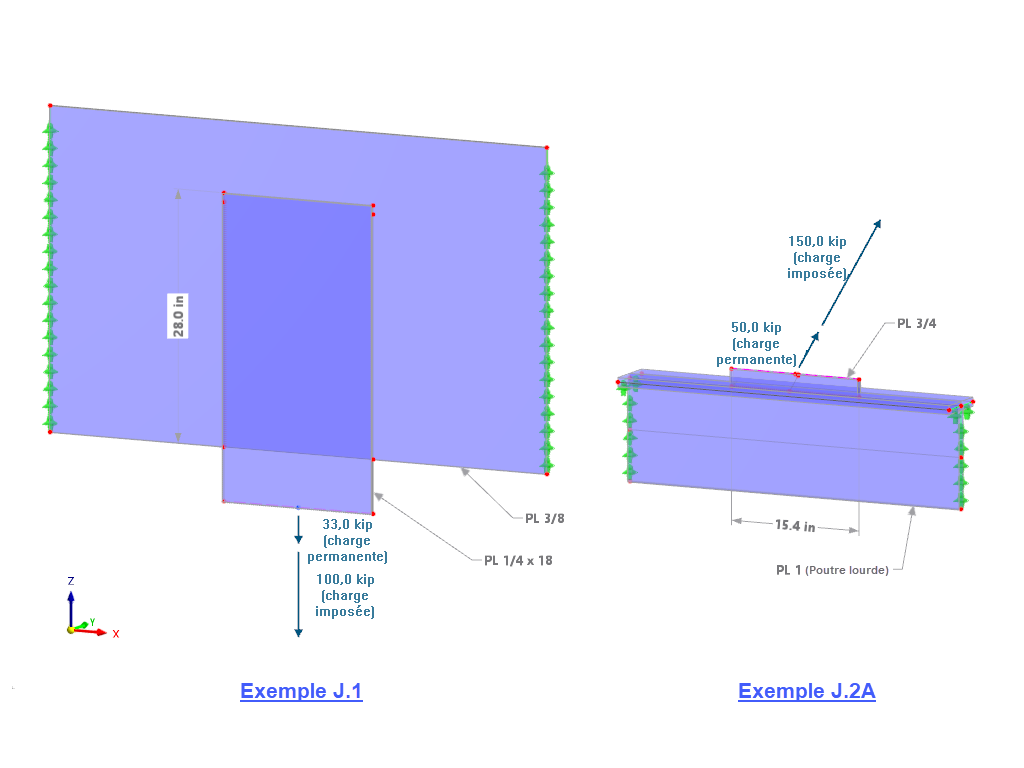
Par souci de simplicité, la rigidité est calculée avec les dimensions indiquées sur la Figure 01.
Structure :
- Longueur du mur l = 2,50 m
- Hauteur du mur h = 2,75 m
- Poteau C24 6/12 cm, ρm,T = 350 kg/m³
- Revêtement OSB 3, t = 18 mm (un côté), ρm, O = 439 kg/m³, G = 108 kN/cm²
- kser = 159 N/mm
- bE = b + t = 12 cm + 1,8cm = 13,8cm
- Agrafes d = 1,5 mm, t = 45 mm
- Distance entre les agrafes av = 60 mm (une rangée)
- Grille = 62,5 cm
- Tirants avec 10 clous, diamètre = 4,2 mm, cloué
- La taille du maillage EF est de 1,3 m. (4 éléments par panneau)
Rigidité :
Flexibilité des fixations (agrafes)
Flexibilité du revêtement
Flexibilité des nervures
Flexibilité de l'ancrage
Somme des flexibilités (calculée sans tirants)
Conversion en surface efficace :
La rigidité calculée est convertie en une rigidité orthotrope efficace du mur. Nous vous recommandons de lire cet article de notre base de connaissance pour obtenir des informations générales sur les matériaux orthotropes.
Composant de rigidité normale
Rigidité de cisaillement dans le plan du mur
Le tirant peut être directement défini dans RFEM sous forme de ressort élastique linéaire avec une rigidité calculée de 6 879,9 N/mm. La comparaison des déformations est illustrée par la Figure 1. Les différences sont également visibles dans le modèle 1 joint à cet article.
La définition des rigidités en flexion d'une plaque peut poser problème lorsque cette méthode est utilisée pour un calcul en 3D. L'article ci-dessus sur les modèles de matériaux orthotropes aborde en détail cet aspect.
Au lieu d'afficher la rigidité du panneau en bois à l'aide de surfaces, la méthode ci-dessous permet de convertir le rendement calculé en une libération linéique.
Cette méthode a pour avantage de considérer les propriétés de surface du modèle comme rigides.
Résumé
Cet article explique comment calculer un panneau en bois à l'aide d'une surface orthotrope efficace. Le tirant peut être directement défini sous forme de rigidité de ressort. Les résultats du calcul linéaire en deux dimensions du système sont très similaires aux calculs manuels de [1]. Il est ainsi possible d'effectuer un calcul réel avec les charges à partir du calcul du raidissement. Le modèle utilisé dans cet exemple est disponible dans la section Téléchargement au bas de cet article.
Cet article décrit également une autre possibilité : convertir la flexibilité en un ressort linéaire de la ligne. Cette méthode convient mieux aux modèles tridimensionnels car elle exclut la majeure partie de l'influence de la flexion de la plaque ainsi que la flexion dans le plan du mur. Ce modèle est également disponible au téléchargement ci-dessous.
Le prochain article de cette série expliquera le raidissement d'un plan au sol en 2D et le calcul 3D d'un mur à ossature bois.
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
