In der ersten Stufe wird bestimmt, wie weit der Schwimmkörper ins Wasser eintaucht. Ist die Eintauchtiefe korrekt bestimmt, dann kann der seitliche Wasserdruck in der zweiten Stufe bis zur Wasserlinie angesetzt werden. Der Auftrieb des Schwimmkörpers kann durch eine elastische Flächenbettung berücksichtigt werden. Eintauchtiefe und Auftrieb hängen linear zusammen. Wenn ein Würfel mit einer Kantenlänge von 1 m komplett ins Wasser eingetaucht wird, dann erzeugt dieser einen Auftrieb von 10 kN. Daraus ergibt sich ein Bettungskoeffizent von cz = 10 kN/m³, der für Bodenflächen angesetzt werden muss.
Damit lässt sich bereits die korrekte Eintauchtiefe bestimmen.
Voraussetzung ist allerdings, dass sich der Schwimmkörper kaum verdreht und die Seitenwände senkrecht sind.
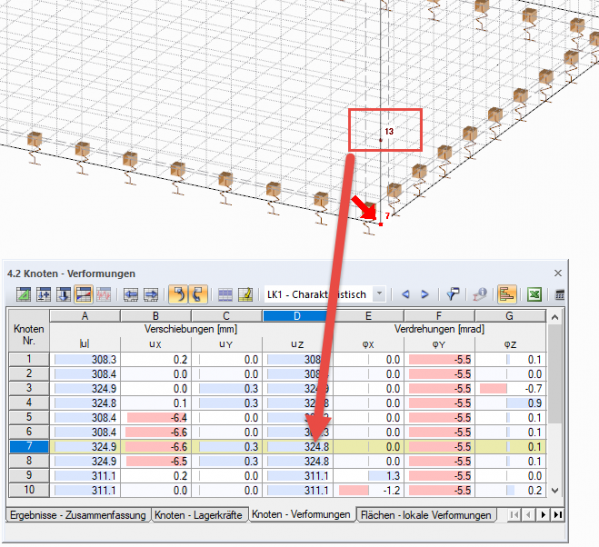
Für jede Lastkombination wird zunächst die Eintauchtiefe festgestellt. Dann wird zu jeder Lastkombination ein zusätzlicher Lastfall hinzugefügt, der jeweils die seitlichen Lasten beinhaltet. Im Beispiel wurde eine Lastkombination LK 1 mit charakteristischen Lasten angelegt. Es ergibt sich für die Knoten 5 und 6 eine Verformung uZ = 308 mm und für die Knoten 7 und 8 uZ = 325 mm. Damit die Lasten einfacher einzugeben sind, wurden an den Stellen jeweils die Hilfsknoten 11 bis 14 angelegt.
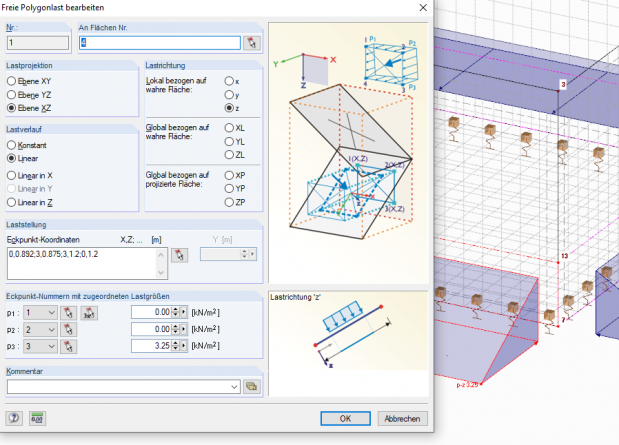
Die Wasserlasten wurden durch freie Polygon-Lasten aufgebracht und aus Gründen der Übersichtlichkeit für jede Last immer nur eine Flächen ausgewählt. Die Lastrichtung ist lokal z. Das bedeutet, dass die Last senkrecht auf der Fläche steht. Der Lastverlauf ist linear. Es müssen dann drei Lastwerte angegeben werden. Gewählt wurden immer zwei Punkte an der Wasseroberfläche, wo die Last Null ist, sowie als dritter Punkt der am tiefsten eingetauchte Punkt und dieser mit 3,25 kN/m² beziehungsweise 3,08 kN/m² beaufschlagt.
Für die Berechnung der Lastkombination wurde aufgrund der recht großen Verformungen Theorie III. Ordnung eingestellt.