Différents principes sont disponibles pour simuler l'interaction sol-structure. Ce chapitre décrit les différentes approches de modélisation par ordre croissant de détail. Il est important de garder à l'esprit que le temps de modélisation et de calcul augmente généralement en raison d'une simulation plus détaillée de l'interaction sol-structure avec une plus grande précision. La figure ci-dessous montre les différentes méthodes.
2D | Méthode du module de réaction
Dans la simulation 2D d'un sol, des ressorts équivalents sont disposés sur la zone de base de la fondation.
Dans la méthode du module de réaction du sol (également fondation Winkler), la rigidité de ces ressorts est décrite comme constante en raison de la relation linéaire entre la contrainte de contact avec le sol et le tassement résultant.
Dans ce cas, la rigidité de cisaillement et le sol adjacent sont négligés, ce qui entraîne un tassement au lieu d'un bassin de subsidence. Ce comportement d'interaction est le plus réaliste pour le sable homogène sec, où la rigidité de cisaillement est très faible.
Différentes modifications de cette méthode ont été développées afin de considérer la rigidité de cisaillement et le sol adjacent, ainsi que pour représenter un comportement de tassement plus réaliste.
2D | La méthode du module de réaction modifié
Les modifications les plus simples augmentent la rigidité du ressort dans la zone du bord de manière simplifiée afin de simuler le raidissement en créant un bassin de subsidence. La figure suivante montre la méthode selon Dörken und Deehne [1] à gauche, où la surface d'un quart de la dimension de fondation est augmentée linéairement jusqu'à la double rigidité. En revanche, il montre l'augmentation du module de réaction du sol selon Bellamann et Katz [2], tandis que dans la rangée des éléments finis extérieure, la rigidité est appliquée, augmentée d'un facteur 4.
Type 2D | La méthode modifiée du module de réaction de fondation à deux paramètres avec extension des fondations
Pour considérer la résistance au cisaillement et les zones de sol adjacentes de manière plus réaliste, le modèle de sol est modifié par l'application d'un dépassement des fondations sans rigidité appropriée. Cela devrait être suffisant pour que le tassement sur son bord soit négligeable. Cette méthode a pour avantage de considérer les fondations adjacentes en plus de la résistance au cisaillement.
Le calcul du module de réaction du sol c1, z dans la direction verticale ainsi que de la résistance au cisaillement c2, v peut être effectué selon les deux méthodes suivantes selon Pasternak ou Barwaschow {%}#Refer [3]]].
|
E0 |
Module d'élasticité du sol suivant |
|
v |
Coefficient de Poisson's du sol in-situ |
|
H |
Épaisseur de la fondation |
|
E0 |
Module d'élasticité du sol suivant |
|
v |
Coefficient de Poisson's du sol in-situ |
|
H |
Épaisseur de la fondation |
Type 2D | La méthode du module de réaction modifié à deux paramètres avec des ressorts équivalents
Selon Kolar et Nemec [5], il est possible d'utiliser la méthode du sol efficace pour simuler un bassin de subsidence en disposant des ressorts supplémentaires. Ces ressorts supplémentaires sont appliqués aux contours et aux points d'angle de la fondation. Elle peut être déterminée à l'aide des formules suivantes.
|
k |
Ressort linéique |
|
K |
Ressort |
|
s0 |
Aire du bassin de subsidence (affaissement d'environ 1% de celui au bord de la fondation) |
|
c2,v |
Capacité de cisaillement (égale ici en x et y) [valeurs de référence de 0,1 c1, z pour le sable meuble à 1,0 c1, z pour la roche solide] |
2D | Méthode du module contraint (demi-espace élastique)
Une simulation encore plus précise du modèle de sol est possible à l'aide de la méthode du module de rigidité (demi-espace élastique) [6]. En déterminant les couches de sol possibles, les zones d'affaissement et en effectuant le calcul itératif de l'interaction sol-structure, cette méthode vous permet de calculer des distributions des coefficients de fondation élastique proches de la réalité.
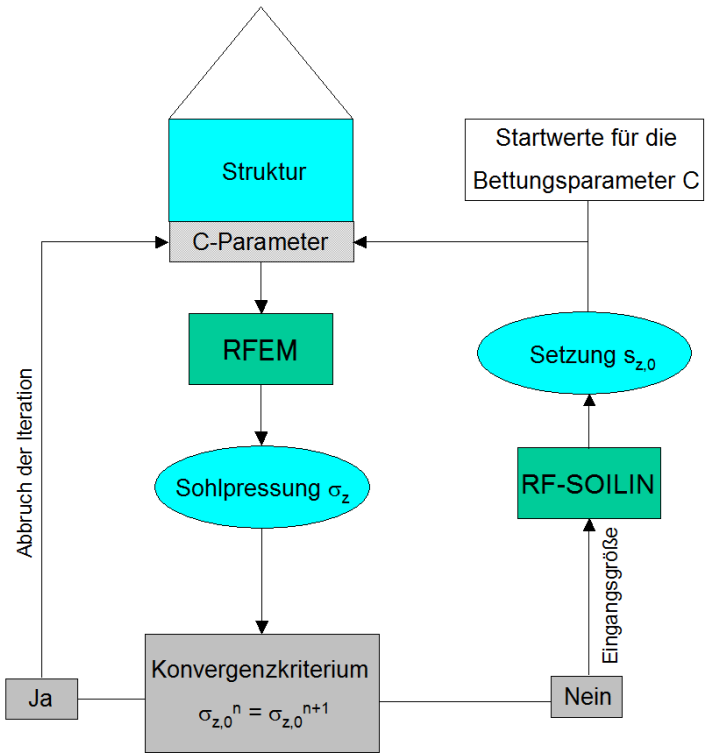
La distribution des paramètres de fondation sous le radier est nécessaire pour le calcul des contraintes de contact avec le sol. En même temps, il dépend de ces compressions. En raison de l'interaction complexe entre le sol et la structure, il est impossible de déterminer les paramètres de fondation dans un simple calcul. La première étape d'itération requiert la sélection des valeurs de départ des paramètres de fondation. Avec ces valeurs de départ, vous pouvez effectuer une analyse aux éléments finis du modèle. On obtient ainsi la distribution des contraintes de contact.
Les contraintes de contact de la première étape d'itération sont incluses comme valeurs initiales pour un autre calcul. Il est possible de calculer le tassement pour chaque élément fini à l'aide des modules d'élasticité des couches de sol entrées. Le tassement et la pression du sol sont utilisés pour calculer les paramètres de fondation. Dans l'étape d'itération suivante, les nouveaux paramètres de fondation remplacent les anciens et une nouvelle analyse aux éléments finis est lancée, qui à son tour
fournit une nouvelle distribution des contraintes de contact. Cette nouvelle distribution est comparée à la première afin d'obtenir un critère de convergence. Tant que l'écart ne dépasse pas une certaine limite de convergence, la nouvelle distribution des contraintes est incluse dans le calcul des nouveaux paramètres de fondation.
Si la différence de la distribution de la pression de surcharge de deux étapes d'itération successives n'est pas atteinte, l'itération est terminée. Les paramètres de fondation de la dernière étape d'itération sont affichés en conséquence. La figure ci-dessous montre le processus de calcul schématique à l'aide de la méthode du module de rigidité (demi-espace élastique).
Les tassements sz sont une valeur intermédiaire importante dans le calcul itératif des paramètres de fondation. Pour la répartition des contraintes dues à la surcharge, le sol est considéré comme un demi-espace homogène avec un matériau isotrope linéaire-élastique selon le modèle de Bossinesq. Ceci est affiché dans la figure ci-dessous. Ici, les composants de tassement sont considérés jusqu'à une profondeur limite résultant soit de l'incrément de contrainte négligeable dû à la surcharge que de la contrainte de poids propre du sol, soit de l'application d'une couche incompressible (par exemple de la roche solide). La contrainte est intégrée par couches. Les tassements sont calculés avec le module de rigidité correspondant. Les paramètres de fondation sont calculés avec la contrainte de contact 𝜎z et les tassements sz.
3D
La simulation la plus réaliste et complexe de l'interaction sol-structure est possible à l'aide de la déformation des conditions de sol existantes dans une analyse 3D aux éléments finis. Toutes les conditions géométriques et de matériau peuvent être considérées ici. Le comportement structurel du sol peut être modélisé à l'aide de {%}002443 modèles de matériau ]] spéciaux selon la réalité. L'interaction des fondations adjacentes est déterminée par leur relation géométrique à l'aide d'un maillage 3D et de compatibilité.