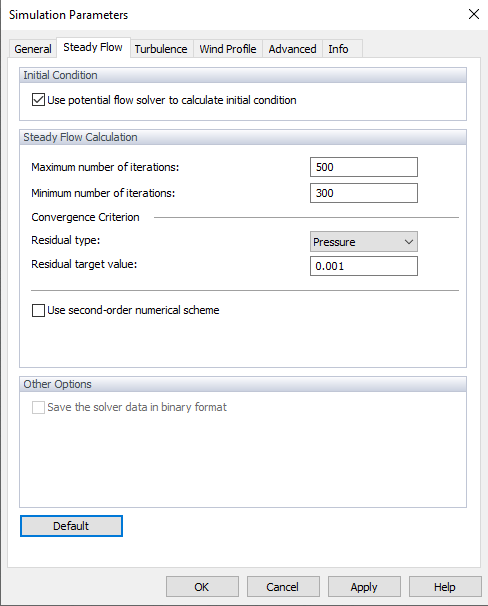
El cálculo del flujo constante se puede seleccionar en la pestaña "General" del cuadro de diálogo "Parámetros de simulación" (ver imagen # extbookmark manual|image029025|Parámetros de simulación #).
Condiciones iniciales
Al activar la opción "Usar flujo potencial para calcular la condición inicial", se usa una versión lineal de las ecuaciones de Navier-Stokes no viscosas para generar las condiciones de inicio.
Cálculo de flujo constante
Puede definir el "Número máximo de iteraciones". De forma predeterminada, el límite es de 500 iteraciones. Si el cálculo converge en menos iteraciones, se detiene. También puede definir "Número mínimo de iteraciones", que se establece en 300 iteraciones de forma predeterminada (ver la imagen # extbookmark manual|imagen029383|Opciones de programa #), independientemente de si ya se ha cumplido el criterio de convergencia (ver más abajo). El número máximo es útil para evitar bucles infinitos.
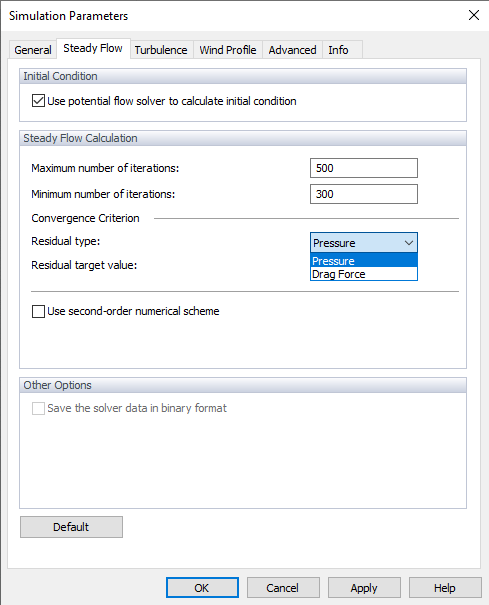
El "Criterio de convergencia" representa el límite de parada para el cálculo. Hay dos criterios de convergencia disponibles, puede seguir el criterio de presión o el criterio de fuerza de arrastre. Seleccione una de las opciones en image033136 Tipo de residuo y luego configure el valor objetivo.
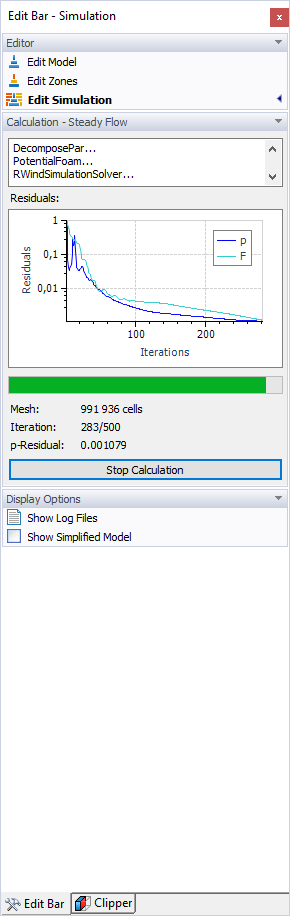
Tan pronto como la cantidad residual descienda por debajo del valor definido, se termina el cálculo. El diagrama de iteraciones y cantidad residual (p-residual para presión) se muestra durante el cálculo. También está disponible en los resultados de la simulación (ver capítulo Residuales ).
La casilla de verificación "Usar esquema numérico de segundo orden" controla qué esquema numérico se usa para los términos de divergencia (flujos). No está activado por defecto, por lo que el cálculo se realiza según el primer orden. Si se ha seleccionado la casilla de verificación, la solución se realiza según el segundo orden.
Otras opciones
El solucionador de estado estable de RWIND 2 no captura completamente los efectos "oscilantes" como se describe en FAQ 4731. Para resolver las ecuaciones diferenciales parciales numéricamente, todos los términos diferenciales (derivadas espaciales y temporales) tienen que estar discretizados. Puede encontrar más información sobre los solucionadores en la documentación de Algorithms and Solvers. Hay una amplia lista de discretizaciones ("esquemas"), y cada esquema tiene un comportamiento numérico particular en vista de la precisión, estabilidad y convergencia. Para obtener más información sobre la convergencia, consulte CFD Direct.