Modelování interakce konstrukce s podložím

Pro simulaci interakce konstrukce s podložím jsou k dispozici různé principy. Tato kapitola popisuje různé přístupy k modelování ve vzestupném pořadí detailů. Je důležité si uvědomit, že doba modelování a výpočtu se obvykle zvyšuje v důsledku podrobnější simulace interakce konstrukce s větší přesností. Na následujícím obrázku jsou znázorněny různé metody.

Schématické znázornění různých modelů půdy pro interakci podloží-konstrukce

2D | Metoda pružinových konstant

Při dvourozměrné simulaci podloží jsou náhradní pružiny uspořádány na základní ploše základu.

Při metodě modulu reakce podloží (také podle Winklerova základu) je tuhost těchto pružin konstantní v důsledku lineárního vztahu mezi kontaktním napětím podloží a výsledným sedáním.

Zde se zanedbá smyková tuhost a přilehlé podloží, takže místo poklesové kotliny vznikne poklesový příkop. Toto interakční chování je nejrealističtější pro suchý homogenní písek, kde je smyková tuhost velmi nízká.
Pro zohlednění smykové tuhosti a přilehlého podloží a pro realističtější průběh sedání byly vyvinuty různé modifikace této metody.

2D | Modifikovaný modul reakce podloží

Nejjednodušší úpravy zvyšují tuhost pružiny v okrajové oblasti zjednodušeným způsobem, aby bylo možné simulovat ztužení vytvořením poklesové kotliny. Na následujícím obrázku je vlevo znázorněna metoda podle Dörkena a Deehna [1], kde se plocha čtvrtiny rozměru základu lineárně zvětšuje na dvojnásobek tuhosti. Naproti tomu ukazuje nárůst modulu podloží podle Bellmanna a Katze [2], zatímco ve vnějším řádku konečných prvků se použije tuhost zvýšená čtyřnásobně.

Modifikovaná metoda modulu reakce podloží

Typ 2D | Upravená dvouparametrická metoda reakce podloží s přesahem podloží

Pro realističtější zohlednění smykové únosnosti a přilehlých oblastí podloží se model podloží upraví tak, že se použije přesah bez příslušné tuhosti. To by mělo být dostatečné, aby sedání na jeho okraji bylo zanedbatelné. Výhodou je, že kromě únosnosti ve smyku lze zohlednit také sousední základy.
Výpočet modulu reakce podloží c_1,z ve svislém směru a smykové únosnosti c_2,v lze provést dvěma následujícími metodami podle Pasternaka nebo Barwaschowa [[#Refer [3{%\] }].

Typ 2D | Modifikovaná dvouparametrická metoda reakce podloží s náhradními pružinami

Podle Koláře a Němce [5] lze simulovat poklesovou kotlinu pomocí přídavných pružin pomocí metody efektivního podloží. Tyto přídavné pružiny jsou aplikovány na obrysy a rohové body základu. Lze ji stanovit podle následujících vzorců.

2D | Metoda vázaného modulu (elastický poloviční prostor)

Ještě přesnější simulaci modelu podloží je možná metoda modulu tuhosti (elastický poloprostor) [6]. Stanovením možných vrstev podloží, poklesové kotliny a iteračním výpočtem interakce konstrukce a podloží umožňuje tato metoda realisticky vypočítat rozdělení součinitelů podloží.

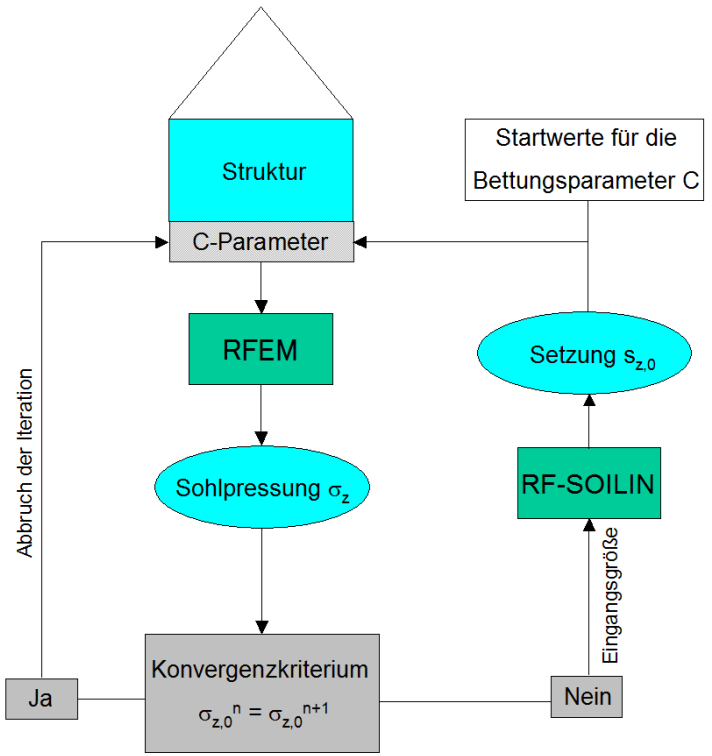
Rozdělení parametrů základu pod základovou deskou je zapotřebí pro výpočet kontaktních napětí v základové spáře. Přitom je na těchto tlakech závislý. Vzhledem ke složité interakci mezi podložím a konstrukcí není možné stanovit parametry základu jednoduchým výpočtem. První iterační krok vyžaduje, aby byly pro parametry základu vybrány počáteční hodnoty. Tyto počáteční hodnoty lze použít pro analýzu modelu metodou konečných prvků. Výsledkem je průběh kontaktních napětí.
Kontaktní napětí v prvním iteračním kroku se zohlední jako počáteční hodnoty pro další výpočet. Spolu se zadanými moduly tuhosti půdních vrstev lze vypočítat sedání pro každý konečný prvek. Pro výpočet parametrů základu se použije sedání a kontaktní napětí. V dalším iteračním kroku nové parametry základu nahradí staré a spustí se nová analýza metodou konečných prvků, která
poskytuje nový průběh kontaktního napětí. Jako kritérium konvergence se porovnává nový průběh napětí se starým. Pokud odchylka neklesne pod určitou mezní hodnotu konvergence, nové rozdělení napětí se zohlední při výpočtu nových parametrů základu.
Pokud není dosaženo rozdílu v rozdělení kontaktních napětí ve dvou po sobě jdoucích iteračních krocích, iterace se ukončí. Zobrazí se tak parametry podloží posledního iteračního kroku. Následující obrázek ukazuje schematický postup výpočtu metodou modulu tuhosti (pružný poloprostor).

Iterativní výpočet parametrů podloží v elastickém poloprostoru

Důležitou mezihodnotou při iteračním výpočtu parametrů základu jsou sedání s_z. Pro rozdělení napětí od přitížení je zemina uvažována jako homogenní poloprostor s lineárně elastickým izotropním materiálem podle modelu Boussinesqa. To je znázorněno na obrázku níže. Přitom se zohledňují složky sedání až do mezní výšky, která vyplývá buď ze zanedbatelného přírůstku napětí v důsledku přitížení ve srovnání s napětím zeminy vlastní tíhou, nebo z použití nestlačitelné vrstvy (např. plné horniny). Napětí se integruje po vrstvách. Poklesy se spočítají společně s příslušným modulem tuhosti. Na základě kontaktního napětí v základové spáře 𝜎_z a sedání s_z se vypočítají parametry podloží.

Šíření napětí v elastickém poloprostoru

3D

Nejrealističtější a nejkomplexnější simulaci interakce konstrukce s podložím lze dosáhnout pomocí deformace stávajících půdních poměrů při 3D analýze konečných prvků. Přitom lze zohlednit libovolné geometrické a materiálové podmínky. Konstrukční chování podloží lze modelovat podle skutečnosti například pomocí speciálních materiálových modelů. Interakce sousedních základů je dána jejich geometrickým vztahem pomocí trojrozměrné sítě a kompatibility.