Un précédent article technique de notre base de connaissance expliquait comment déterminer les propriétés de matériau du béton fibré et convertir ces paramètres de matériau dans le logiciel de calcul de structure aux éléments finis RFEM.
Le béton fibré est aujourd'hui principalement utilisé pour les sols industriels et les radiers à faibles sollicitations. La détermination élastique linéaire des efforts internes ne fournit pas de résultats économiques pour les composants structuraux fabriqués dans ce matériau. Les méthodes plastiques sont donc généralement utilisées à l’état limite ultime. Les approches plastiques ne conviennent cependant pas à l’état limite de service. Un calcul non linéaire selon la méthode des éléments finis est toujours possible quel que soit l’état limite à étudier. Un calcul manuel est ensuite effectué à l’aide des efforts internes déterminés de manière itérative.
Entrée de la topologie et des charges
Le radier est entré sous forme de fondation surfacique. Le radier de cet article technique est réalisé à l’aide de la méthode du « sol efficace » selon Kolar et Nemec [3]. Le sol adjacent est considéré à l’aide de ressorts linéiques supplémentaires et de ressorts simples aux coins (voir cet article technique).
Il est également possible de calculer la fondation élastique à l’aide du module additionnel RF-SOILIN.
La vérification à l’ELU est indiquée en fonction des charges provenant des montants et des charges sous les rayonnages. Les charges des montants sont définies comme des charges rectangulaires libres. Des points avec raffinement de maillage ont en outre été définis sur les montants afin que la charge soit répartie sur plusieurs éléments dans la semelle.
Définition des propriétés de matériau
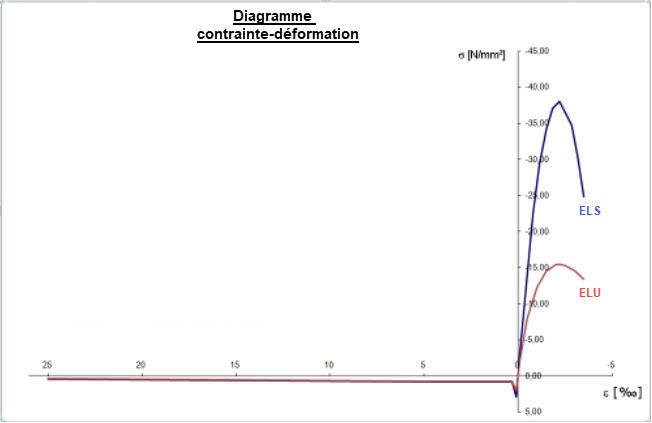
Le modèle de matériau « Endommagement isotrope 2D/3D » du module additionnel RF-MAT NL est idéal pour représenter le comportement du béton fibré dans RFEM. Le béton fibré utilisé est un béton C30/37 L1.2/L0.9 conformément à la norme DIN EN 1992-1-1 [2] et aux lignes directrices du Commission allemande de Béton armé (DAfStb) sur du béton fibré [1] avec les deux classes de performance L1/L2 = L1,2/L0,9. Pour un calcul non linéaire, la courbe parabolique selon 3.1.5 [2] doit être utilisée sur le côté correspondant à la compression du diagramme contrainte-déformation. La figure suivante montre l'évolution caractéristique de la courbe de travail du béton fibré.
C'est la courbe caractéristique de contrainte-déformation qui doit être utilisée pour l'ELS. Pour le calcul non linéaire à l’ELU, les dispositions suivantes du Chapitre 5.7 de la Deutsche Ausschuss für Stahlbeton (DAfStb, Commission allemande du béton armé) concernant le béton fibré [1] doivent être appliquées :
| 1,04 ⋅ ffcrLi | Valeur moyenne calculée de la contrainte de traction qui peut être absorbée par le béton fibré après fissuration selon les classes de performance L1 ou L2 |
| fcR, fyR, ftR | Valeur moyenne respective de la résistance du béton selon NA.10, DIN EN 1992-1-1 |
| γR | Coefficient partiel de sécurité pour la résistance du système |
γR est supposé être de 1,4 pour les composants en béton fibré.
Le facteur de sécurité partiel γR peut être considéré sur le côté en résistance lors de l'entrée des propriétés du matériau ou du côté de l'action. Dans cet article, le facteur de sécurité partiel global γR est appliqué directement lors de la définition de la courbe de travail non linéaire. La Figure 03 montre la courbe contrainte-déformation réduite pour la vérification à l’ELU par rapport à la courbe de travail caractéristique à l’ELS.
Pour les calculs non linéaires, la charge doit être appliquée par incrément. Si le calcul d’un incrément de charge ne converge pas au cours du nombre maximal d’itérations prédéfini, le nombre maximal d’itérations doit être augmenté dans les paramètres de calcul. Une meilleure convergence lors de l’utilisation d'un modèle de matériau non linéaire peut également être obtenue en sélectionnant le solveur d’équations non symétrique dans les paramètres de calcul.
Vérification à l’ELU
L’état limite ultime est considéré comme atteint si :
- les déformations ultimes du béton fibré, εcu1 du côté en compression et εfct,u du côté en traction, sont atteintes ;
- l’état critique d'équilibre indifférent est totalement ou partiellement atteint au sein du système global.
Une fois le calcul non linéaire de la semelle effectué avec succès, les déformations maximales et minimales de la face supérieure et inférieure sont vérifiées. Si les déformations limites ne sont pas dépassées, la vérification à l’ELU est effectuée.
Les déformations suivantes ont été calculées à l’ELU :
Face supérieure :
- déformation maximale en compression εmin- = -1,9 ‰ <3,5 ‰
- déformation maximale en traction εmax- = 4,2 ‰ <25,0 ‰
Face inférieure :
- déformation maximale en compression εmin + = -1,05 ‰ <3,5 ‰
- déformation maximale en traction εmax + = 9,9 ‰ <25,0 ‰
La Figure 05 montre la déformation maximale sur le côté supérieur (-z) du radier.
Le respect des déformations limites a permis de déterminer avec succès l’ELU en flexion. Des vérifications supplémentaires à l’ELU doivent cependant être effectuées, par exemple pour le poinçonnement.
Recommandations pour le calcul non linéaire avec le modèle de matériau « Endommagement isotrope 2D/3D »
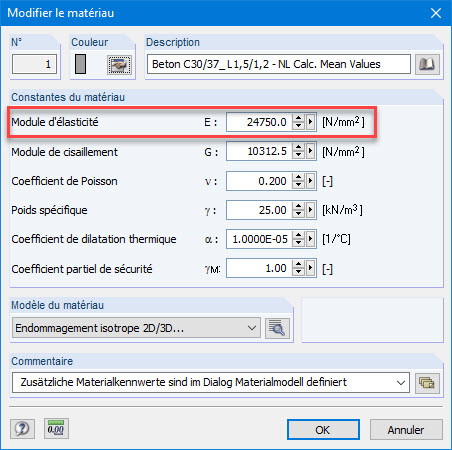
Selon la définition polygonale de la courbe contrainte-déformation sous forme de diagramme, le module tangent à l'origine de la courbe contrainte-déformation doit être le module d'élasticité du béton fibré dans RFEM. Cela signifie que le module sécant prédéfini pour le béton doit également être ajusté lors de l’entrée sur la courbe de travail du béton fibré. Le module d’élasticité du matériau est attendu comme pente par le premier point polygonal du côté en compression ou traction de la courbe de travail.
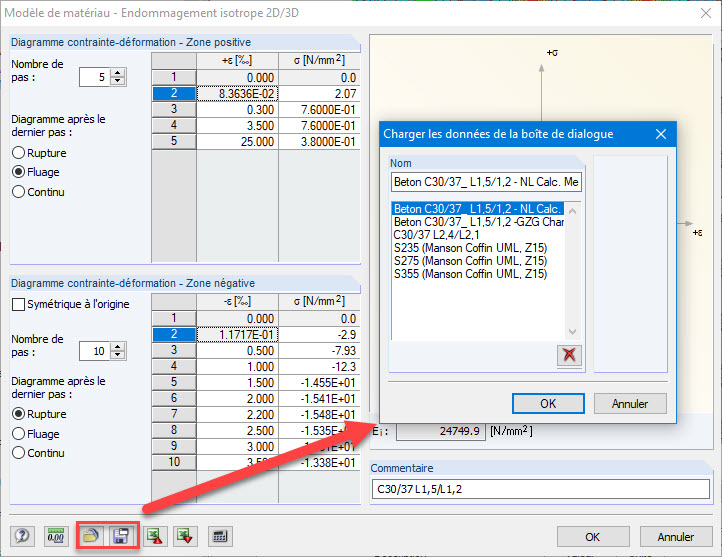
Le fichier Excel disponible au téléchargement au bas de cet article technique facilite la saisie et le calcul des points du diagramme. En fonction de l’état limite analysé (ELU ou ELS), ce fichier Excel permet de déterminer la courbe contrainte-déformation à utiliser et de la transférer dans la boîte de dialogue d'entrée de RFEM à l'aide du presse-papiers. Cette opération est expliquée dans la vidéo ci-contre.
Les diagrammes contrainte-déformation définis peuvent être enregistrés dans RFEM et réutilisés dans d’autres projets. On peut ainsi créer une bibliothèque de matériaux personnalisée pour les bétons fibrés dans RFEM.
En raison de la non-linéarité importante, la charge doit être appliquée en plusieurs incréments de charge. Le nombre d’incréments de charge doit être sélectionné de sorte que le système reste à l’état élastique linéaire lors du premier incrément de charge. Cela améliore la convergence du calcul. Le nombre d’incréments de charge global peut être contrôlé dans les paramètres de calcul et le nombre d’incréments local pour chaque combinaison de charges ou cas de charge. 20 incréments de charge s’avèrent adéquats pour l’itération de la charge de vérification à l’ELU du radier. 20 incréments de charge ont été définis localement pour la combinaison de charges (Figure 08).
Base de connaissance