Neste artigo, também é altamente recomendado não criar somente um modelo de EF único para todas as cascas em aço, definir as cargas e de seguida clicar em "Calcular". Na maioria dos casos, este procedimento gera trabalho adicional, uma vez que estão disponíveis numerosos métodos analíticos para a verificação de casos simples que são comuns na prática de dimensionamento. Estes métodos analíticos, as fórmulas de cálculo manual, também têm a grande vantagem de poupar espaço e de uma documentação simples. Para alguns recipientes, é possível realizar a análise de encurvadura local de placas numa página A4. Tal economia de espaço para a documentação não é possível com a análise de EF.
No entanto, também existem inúmeros casos em que o uso de uma análise de elementos finitos faz sentido e deve ser preferido em relação a um cálculo manual. Os seguintes pontos são apenas alguns exemplos de casos onde faz sentido utilizar um cálculo de EF:
No seguinte texto, a verificação da encurvadura de uma casca de aço é realizada através do RFEM de acordo com o conceito MNA/LBA. Assim, é aplicado um comportamento material não linear do aço.
Verificação da encurvadura local de placas de acordo com EN 1993-1-6
Na norma EN 1993-1-6, são apresentadas três opções para a realização da verificação de encurvadura local da placa para estruturas em cascas de aço. Nesta secção, devem ser listados de forma resumida e avaliados em relação aos requisitos da tecnologia de cálculo, bem como em relação aos requisitos para o engenheiro de dimensionamento.
Verificação da encurvadura local de placas baseada na tensão
A verificação da encurvadura local de placas baseada nas tensões é considerada como método de verificação padrão, o qual quase todos os engenheiros já utilizaram quando realizaram o dimensionamento de estruturas em casca. Um engenheiro qualificado classifica este método como fácil e os requisitos de cálculo são muito baixos ou inexistentes, uma vez que são frequentemente utilizadas fórmulas para o cálculo manual.
Um grande problema deste método de verificação é que dificilmente serão alcançados resultados económicos para estruturas em casca com situações de cargas que variam de forma significativa dos modos de encurvadura padrão. Para além disso, o utilizador deste conceito encontra-se num caminho errado com este método, porque pode facilmente chegar a conclusão que a segurança a encurvadura local da estruturas em casca depende apenas das tensões ocorrentes. Se esse fosse o caso, o reforço de uma parede de casca através de nervuras longitudinais, por exemplo, não produziria grandes benefícios, pois esta opção não reduziria significativamente as tensões. Na realidade, a segurança a encurvadura local de uma casca habilmente reforçada é muito maior do que a de uma casca sem reforço com uma espessura de parede igual.
Verificação da encurvadura local baseada numa análise numérica através do cálculo global MNA/LBA
Este método será utilizado para o seguinte dimensionamento da estrutura em casca. Um cálculo MNA/LBA certamente requer que o utilizador tenha um pouco mais de conhecimento prévio em estabilidade de cascas do que para o caso do método de dimensionamento baseado na tensão. Além do mais, a técnica computacional deve ser mais poderosa uma vez que tem de ser realizada uma análise linear elástica bifurcada (LBA) e uma análise não linear do material (MNA) para a aplicação correta deste método.
Na visão do autor, este método de dimensionamento é a forma mais eficaz de realizar a análise de encurvadura local de placas, partindo do princípio, que deve ser utilizada uma análise de EF. A justificação para isso é que, para um dimensionamento utilizando o conceito MNA/LBA, a tecnologia de cálculo é utilizada de forma consistente sem esperar muito esforço por parte do utilizador. Se as forças internas da estrutura em casca forem calculadas de forma linear elástica, para depois as utilizar na análise de encurvadura local baseada em tensões, a técnica de cálculo é, porém, utilizada de forma demasiado inconsistente, uma vez que programas poderosos como o RFEM estão capacitados a determinar também a carga resistente de estruturas de casca.
Verificação da encurvadura local baseada numa análise numérica através do cálculo global GMNIA
A análise GMNIA para determinar estabilidade suficiente das estruturas em casca, é provavelmente o método mais consistente da verificação de encurvadura local. As forças internas são assim calculadas de forma geométrica e com material não linear, utilizando imperfeições.
Este método requer um excelente conhecimento teórico da estabilidade de estruturas em casca por parte do utilizador, entre outras coisas, uma abordagem correta das imperfeições (pré-encurvadura) é muito complexa. Se o utilizador não tiver esses conhecimentos prévios, o processo de dimensionamento com o conceito GMNIA deve ser evitado em qualquer caso. Além do mais, são colocadas sobre a técnica de cálculo elevadas exigências aquando da utilização deste método. Assim, o programa utilizado deve ser capaz de realizar a análise de bifurcação para cada passo de carga da análise não linear para, quando apropriado detetar um "salto" do percurso pré-encurvadura sub-crítico para o caminho pós-encurvadura supra crítico.
Este conceito não será mais aqui explicado, uma vez que na visão do utilizador tem pouca importância para a prática de dimensionamento. Para mais informações, consulte o artigo de Herbert Schmidt [2] no Steel Construction Calendar de 2012, que oferece uma boa visão geral das dificuldades enfrentadas ao utilizar o dimensionamento de acordo com o método GMNIA.
Exemplo de uma verificação de encurvadura local através do método MNA/LBA
Entrada do sistema estrutural
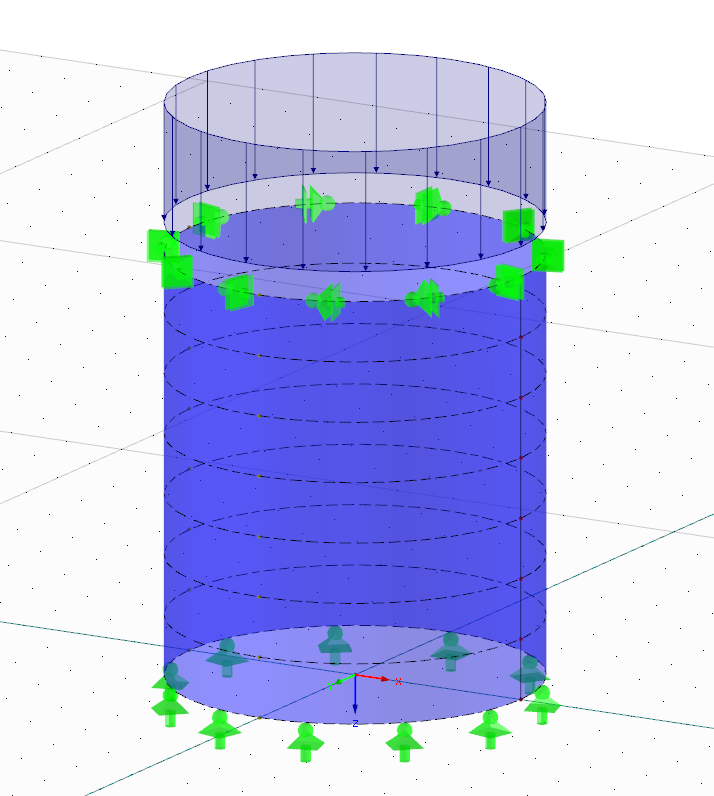
A estrutura em casca de aço apresentada na Figura 01 será verificada a encurvadura local. Em princípio, esta estrutura é um caso típico em que um engenheiro familiarizado com o dimensionamento de cascas de aço dificilmente consideraria uma análise de EF. Uma vez que o principal objetivo deste artigo é de familiarizar o leitor com o tópico da verificação da encurvadura local de acordo com o conceito MNA/LBA, será utilizado um exemplo simples.
Um importante tópico no cálculo não linear ou na análise bifurcada de estruturas em casca é o tamanho do elemento, uma vez as definições da malha de EF selecionadas de forma desfavorável conduzem a resultados enganadores. Na literatura especializada, existem várias fórmulas para um cálculo aproximado, sendo que que a abordagem provavelmente mais sensata, é um (pequeno) estudo de convergência.
Cálculo com o RFEM
Após a introdução do modelo e do carregamento e a adequada seleção das definições da malha de EF, pode iniciar o cálculo com o RFEM. Primeiro, é realizada a análise não linear do material. O objetivo desta análise é a resistência plástica de referência, isto é, o coeficiente de carga crítica ao qual toda a casca entrará em cedência e forma plástica. O ideal é utilizar o módulo adicional RF-MAT NL, pois só assim ficam disponíveis no RFEM propriedades de material não-lineares. Em alternativa, pode ser realizado um cálculo elástico linear; então, a resistência de referência plástica pode ser calculada aproximadamente utilizando a fórmula (8.24) de [3]. A Figura 02 mostra o sistema deformado após atingir a resistência plástica de referência rRpl = 11,90.
Posteriormente, é realizada a análise linear bifurcada, sendo que a sequência foi aqui escolhida de forma arbitrária. Também é possível realizar esta análise primeiro e depois continuar com o método MNA. O objetivo da análise linear bifurcada é também o de obter um coeficiente de carga crítica, mas desta vez um que cause a encurvadura local de uma casca perfeita. Isso requer o módulo adicional RF-STABILITY, com o qual podem ser realizadas análises de bifurcações lineares e cálculos geometricamente não lineares. Isso não se refere aos cálculos do GMNIA. A Figura 03 apresenta a primeira forma própria da casca considerada para o valor próprio de rRcr = 7,70.
Verificação de encurvadura local
A verificação da encurvadura local é apresentada na íntegra a seguir. Deve ser dada especial atenção aos quatro parâmetros de encurvadura independentes, que podem ser determinados para a maioria dos casos de construção práticos de acordo com o anexo D em [3].
Resistência de referência plástica da MNA:
rRpl = 11,9
Fator de carga crítica da LBA:
rRcr = 7,70
Grau de esbelteza:
Fator de imperfeição elástico:
Fator de multiplicação plástico:
βov = 0,60
Expoente da curva de encurvadura:
ηov = 0,60
Grau limite de esbelteza totalmente plástico:
Esbelteza limite parcialmente plástica:
Fator de redução da encurvadura:
Verificação da encurvadura local:
O principal problema do dimensionamento é classificar os resultados obtidos pelo programa num dos casos típicos de encurvadura. No caso vertente, é muito simples devido ao carregamento: Trata-se de encurvadura por pressão meridiana pura. Assim, são calculados os parâmetros de encurvadura independentes de acordo com o anexo D 1.2 da EN 1993-1-6 [3].
O resultado da análise de encurvadura local de acordo com o método MNA/LBA é um fator de carga crítico. No exemplo apresentado aqui, é 1,515. Isto é, A carga da casca podia ser aumentada em mais de 50%.
Sendo a verificação efetuada com o conceito baseado nas tensões, o resultado seria um coeficiente de carga crítica de 1.398, o que mostra que para os casos de encurvadura típica, tais como a encurvadura de pressão no meridiano considerada aqui, não se obtém benefícios adicionais através da análise de encurvadura local de placas baseada numericamente de acordo com o método MNA/LBA. De notar, como já mencionado, que isto é diferente assim que as introduções de carga ou apoios locais conduzem a concentrações de tensões.
Conclusão
Os programas de EF modernos, intuitivos e poderosos tais como o RFEM, facilitam significativamente o trabalho de um engenheiro na realização das verificações a segurança de encurvadura suficiente de uma estrutura em casca. Como resultado de uma utilização mais consistente da tecnologia informática no conceito MN/LBA, geralmente podem ser alcançados resultados mais realistas e, portanto, mais económicos.
Deve ser mencionado que uma análise de EF não é aconselhável para estruturas em casca muito pequenas, uma vez que se encontram disponíveis métodos analíticos de igual forma competentes para os casos de encurvadura típicos, os quais podem levar a documentação reduzida e ao mesmo tempo a resultados igualmente económicos. Contudo, se o engenheiro se depara com casos no dimensionamento prático que não podem ser atribuídos a uma caso de encurvadura típico, uma análise de EF de acordo com o conceito MNA/LBA com o RFEM e os módulos adicionais RF-STABILITY e RF-MAT NL é uma alternativa real aos métodos clássicos.