In questo articolo, consigliamo vivamente di non creare semplicemente un singolo modello EF per ciascun guscio in acciaio, impostare i carichi e quindi premere "Calcola". Nella maggior parte dei casi, questa procedura porta a un lavoro aggiuntivo, poiché sono disponibili numerosi metodi analitici per la verifica per casi semplici che sono comuni nella pratica di progettazione. Questi metodi analitici, le formule di calcolo manuale, hanno anche il grande vantaggio di una documentazione semplice e salvaspazio. Per alcuni contenitori, l'analisi di instabilità della piastra può essere eseguita su una pagina A4. Tale documentazione salvaspazio non è possibile con un'analisi EF.
Tuttavia, ci sono anche numerosi casi in cui l'uso di un'analisi agli elementi finiti ha senso e dovrebbe essere preferito rispetto a un calcolo manuale. I seguenti punti sono solo alcuni esempi di casi in cui ha senso utilizzare un calcolo EF:
Nel testo seguente, la verifica dell'instabilità di un guscio in acciaio viene eseguita utilizzando RFEM secondo il concetto MNA/LBA. Pertanto, viene applicato il comportamento non lineare del materiale dell'acciaio.
Analisi di instabilità delle piastre secondo EN 1993-1-6
Nella EN 1993-1-6, sono presentate tre opzioni per eseguire un'analisi di instabilità delle piastre per gusci di acciaio. In questa sezione, devono essere brevemente elencati e valutati rispetto ai requisiti della tecnologia informatica, nonché rispetto ai requisiti imposti all'ingegnere progettista.
Analisi di instabilità della piastra basata sulla tensione
L'analisi di instabilità della piastra basata sulle tensioni è considerata il metodo di analisi standard che quasi tutti gli ingegneri hanno utilizzato durante l'esecuzione della progettazione di gusci. Un ingegnere esperto classifica questo metodo come facile e i requisiti di calcolo sono molto bassi o inesistenti, poiché vengono spesso utilizzate formule per il calcolo manuale.
Uno dei principali problemi di questo metodo di analisi è che i risultati economici saranno difficilmente raggiunti per strutture a guscio con situazioni di carico che si discostano notevolmente dai modi di instabilità standard. Inoltre, come utente di questo concetto, si è sulla strada sbagliata con questo metodo, perché si potrebbe facilmente pensare che la sicurezza all'instabilità della piastra della struttura a guscio dipenda solo dalle tensioni che si verificano. Se così fosse, l'irrigidimento di una parete a guscio, ad esempio, mediante nervature longitudinali avrebbe scarso vantaggio, poiché ciò non riduce significativamente le tensioni. In realtà, la sicurezza all'instabilità della piastra di un guscio abilmente irrigidito è molto più alta di quella di un guscio non controventato con lo stesso spessore della parete.
Analisi di instabilità della piastra basata sul calcolo numerico per mezzo del calcolo MNA/LBA globale
Questo metodo sarà utilizzato per la seguente verifica a guscio. Un calcolo MNA/LBA richiede certamente che l'utente abbia una conoscenza di base nella stabilità del guscio rispetto al metodo di verifica basato sulle tensioni. Inoltre, la tecnica di calcolo dovrebbe essere più potente, poiché un'analisi di biforcazione elastica lineare (LBA) e un'analisi non lineare del materiale (MNA) devono essere eseguite per una corretta applicazione di questo metodo.
Secondo l'autore, questo metodo di verifica è il modo più efficace per eseguire l'analisi di instabilità della piastra se il calcolo deve essere eseguito utilizzando l'analisi EF. La giustificazione di ciò è che per un progetto che utilizza il concetto MNA/LBA, la tecnologia informatica viene utilizzata in modo coerente senza aspettarsi troppi sforzi da parte dell'utente. Se le forze interne del guscio sono calcolate in modo elastico lineare per utilizzarle per l'analisi di instabilità della piastra basata sulle tensioni, la tecnologia informatica sarà utilizzata in modo troppo incoerente, poiché programmi potenti come RFEM sono anche in grado di determinare la capacità portante del struttura a guscio.
Analisi di instabilità della piastra basata sul calcolo numerico per mezzo del calcolo GMNIA globale
Un'analisi GMNIA per determinare una stabilità sufficiente del guscio è probabilmente il metodo più coerente di analisi di instabilità delle piastre. Le forze interne sono quindi calcolate geometricamente e materialmente in modo non lineare, utilizzando le imperfezioni.
Questo metodo richiede un'eccellente conoscenza di base sulla stabilità del guscio da parte dell'utente, poiché, tra le altre cose, il corretto approccio alle imperfezioni (pre-instabilità) è molto difficile. Se l'utente non ha queste conoscenze di base, il processo di progettazione con il concetto GMNIA dovrebbe essere evitato in ogni caso. Inoltre, quando si utilizza questo metodo, vengono poste richieste sostanziali alla tecnologia informatica. Pertanto, il sistema di programma utilizzato deve essere in grado di eseguire un'analisi di biforcazione per ogni fase di carico dell'analisi non lineare per, se del caso, rilevare un "salto" dal percorso pre-instabilità subcritico al percorso post-instabilità supercritico.
Questo concetto non sarà spiegato ulteriormente qui, poiché, secondo l'autore, ha poco significato per la pratica di progettazione. Per ulteriori informazioni, fare riferimento all'articolo di Herbert Schmidt [2] nel Calendario delle costruzioni in acciaio del 2012, che offre una buona panoramica delle difficoltà incontrate quando si utilizza la verifica secondo il metodo GMNIA.
Esempio di analisi di instabilità delle piastre utilizzando il metodo MNA/LBA
Input del sistema strutturale
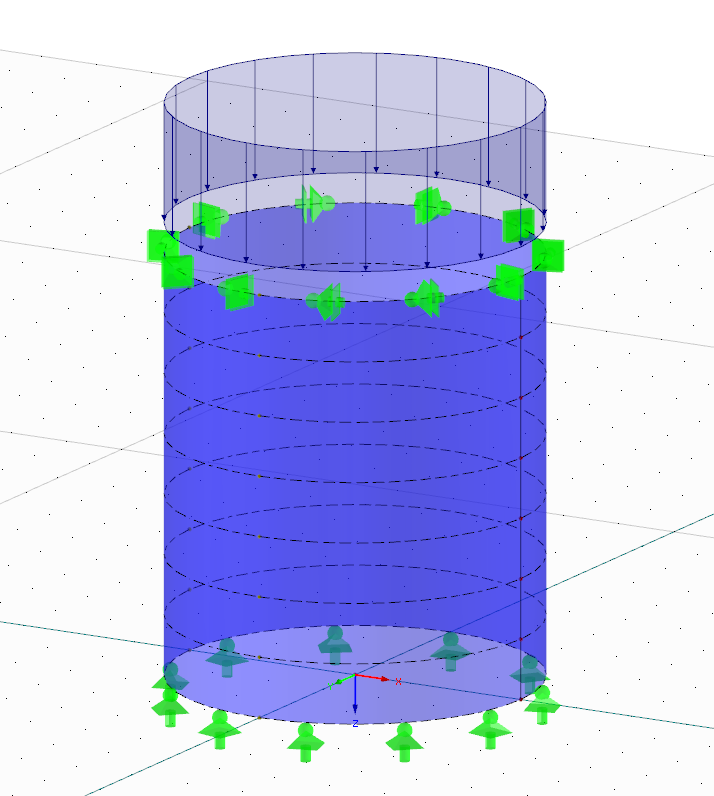
Il guscio in acciaio mostrato nella Figura 01 sarà progettato per instabilità. In linea di principio, questa struttura è un caso tipico in cui un ingegnere che ha familiarità con la progettazione di gusci in acciaio difficilmente considererebbe un'analisi EF. Poiché lo scopo principale di questo articolo è quello di familiarizzare il lettore con l'argomento dell'analisi di instabilità delle piastre secondo il concetto MNA/LBA, verrà utilizzato un esempio il più semplice possibile.
Un argomento importante nei calcoli non lineari o nelle analisi di biforcazione delle strutture a guscio è la dimensione dell'elemento, poiché le impostazioni della mesh EF selezionate in modo sfavorevole possono portare a risultati falsificati. Nella letteratura specializzata, esistono varie formule per il calcolo approssimativo per questo, dove lo studio di convergenza (piccolo) è l'approccio più appropriato.
Calcolo con RFEM
Dopo aver inserito il modello e il carico e aver selezionato le impostazioni della mesh EF adatte, il calcolo con RFEM può iniziare. Innanzitutto, viene eseguita l'analisi non lineare del materiale. Lo scopo di questa analisi è la resistenza plastica di riferimento (cioè il coefficiente di carico critico al quale l'intero guscio si rompe plasticamente). Il modulo aggiuntivo RF-MAT NL è idealmente utilizzato, poiché in RFEM sono disponibili solo le proprietà non lineari del materiale. In alternativa, è possibile eseguire un calcolo elastico lineare; allora la resistenza di riferimento plastica può essere calcolata approssimativamente utilizzando la formula (8.24) da [3]. La Figura 02 mostra il sistema deformato dopo aver raggiunto la resistenza di riferimento plastica rRpl = 11,90.
Successivamente, viene eseguita l'analisi della biforcazione lineare dove la sequenza è stata scelta arbitrariamente qui. È anche possibile eseguire prima questa analisi, quindi continuare con il metodo MNA. Lo scopo dell'analisi della biforcazione lineare è anche quello di ottenere un coefficiente di carico critico, ma questa volta che causerebbe l'instabilità del guscio perfetto. Ciò richiede il modulo aggiuntivo RF-STABILITY, con il quale è possibile eseguire analisi di biforcazione lineare e calcoli geometricamente non lineari. Questo non si riferisce ai calcoli GMNIA. La Figura 03 mostra la prima forma modale del guscio considerato per l'autovalore di rRcr = 7.70.
Analisi di instabilità delle piastre
L'analisi di instabilità della piastra è mostrata nel suo insieme nel testo seguente. Particolare attenzione deve essere prestata ai quattro parametri di instabilità indipendenti, che possono essere determinati per la maggior parte dei casi pratici di costruzione secondo l'Appendice D in [3].
Resistenza di riferimento plastica dall'MNA:
rRpl = 11,9
Coefficiente di carico critico dall'LBA:
rRcr = 7.70
Grado di snellezza:
Coefficiente di imperfezione elastica:
Coefficiente di moltiplicazione plastico:
βov = 0,60
Esponente della curva di instabilità:
ηov = 0,60
Grado di snellezza limite completamente plastico:
Snellezza limite parzialmente plastica:
Coefficiente di riduzione dell'instabilità:
Analisi di instabilità della piastra:
Il problema principale della verifica è quello di classificare i risultati ottenuti dal programma in uno dei tipici casi di instabilità. In questo caso, è molto semplice a causa del carico: Si tratta di pura instabilità da pressione del meridiano. Pertanto, vengono calcolati i parametri di instabilità indipendenti secondo l'Appendice D 1.2 in EN 1993-1-6 [3].
Il risultato dell'analisi di instabilità della piastra secondo il metodo MNA/LBA è un coefficiente di carico critico. Nell'esempio mostrato qui, è 1.515. Ciò significa: Il carico del guscio potrebbe essere aumentato di oltre il 50%.
Se l'analisi si basa sul concetto di tensione, ciò risulterebbe in un coefficiente di carico critico di 1.398, il che mostra che per i casi di instabilità tipici, come l'instabilità da pressione del meridiano qui considerato, non si ottengono vantaggi aggiuntivi dalla piastra basata numericamente analisi di instabilità secondo il metodo MNA/LBA. Va notato, come già accennato, che questo è diverso non appena le introduzioni di carichi locali o i vincoli esterni portano a concentrazioni di tensioni.
Conclusione
Programmi FEM moderni, potenti e intuitivi come RFEM facilitano notevolmente il lavoro di un ingegnere calcolatore durante la verifica della sicurezza sufficiente all'instabilità di un guscio. Come risultato dell'uso più coerente della tecnologia informatica nel concetto MN/LBA, generalmente è possibile ottenere risultati più realistici e quindi più economici.
Va anche menzionato che un'analisi EF non è consigliabile per ogni struttura a guscio, poiché sono disponibili buoni metodi analitici per casi di instabilità tipici, che possono portare a una documentazione ridotta e a risultati altrettanto economici. Tuttavia, se l'ingegnere incontra casi nella pratica di progettazione che non possono essere assegnati a un caso di instabilità tipico, un'analisi EF secondo il concetto MNA/LBA con RFEM con i moduli aggiuntivi RF-STABILITY e RF-MAT NL è un vero problema alternativa ai metodi standard.