Der Empfindlichkeitsbeiwert θ ist wie folgt definiert [1]:
| θ | Coeficiente de sensibilidade de deslocamento entre pisos |
| Ptot | Carga de gravidade total no piso e acima, considerado na situação de cálculo sísmica |
| dr | Deslocamento entre pisos de cálculo determinado como diferença dos deslocamentos laterais médiosds na parte superior e inferior do piso em questão; neste caso, os deslocamentos são determinados através do espectro de resposta de cálculo linear com q = 1,0 |
| Vtot | Corte sísmico total de piso determinado utilizando o espectro de resposta de cálculo linear |
| h | Altura do piso |
Os efeitos de segunda ordem podem ser considerados aproximadamente por um fator igual a 1/(1 - θ), se 0,1 < θ ≤ 0,2. Para θ > 0,2, é necessário considerar a matriz de rigidez geométrica ao calcular os valores próprios e a análise de espectro de resposta multimodal.
Matriz de rigidez geométrica
Para as análises dinâmicas, os cálculos iterativos para a determinação não linear da teoria de segunda ordem não são adequados. O problema pode ser linearizado e basta utilizar a matriz de rigidez geométrica com base nas cargas axiais para considerar a teoria de segunda ordem. Dabei wird angenommen, dass die vertikalen Lasten sich aufgrund horizontaler Einwirkungen nicht ändern und die Verformungen klein sind verglichen mit den Gebäudeabmessungen [2]. Die zu berücksichtigenden Lasten sollten denen der Bemessungssituation für Erdbeben nach EN 1990 Abschnitt 6.4.3.4 [3] entsprechen:
Onde
Ed = valor de cálculo dos efeitos
Gk,j = valor característico da ação permanente j
Qk,i = valor característico da ação variável i
Ψ2,i = fator para os valores quase-permanentes das ações variáveis i
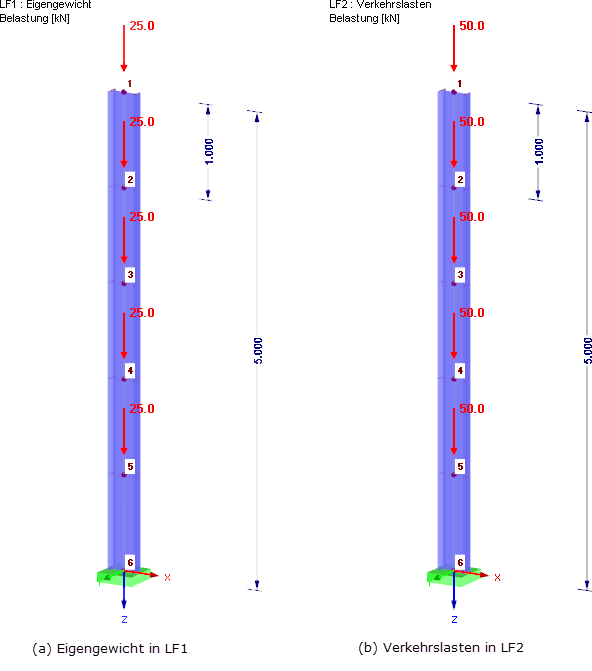
As forças de tração axiais aumentam a rigidez, por exemplo, num cabo pré-esforçado. As forças de compressão reduzem a rigidez e podem levar a uma singularidade na matriz de rigidez. Die geometrische Steifigkeit Kg ist nicht abhängig von den mechanischen Eigenschaften des Systems, sondern nur von Länge L und Normalkraft N im Stab. Para ilustrar o problema de base, é apresentado um exemplo simples de uma consola na Figura 01. Os pontos de massa individuais da consola representam os pisos individuais do edifício. O edifício é sujeito a uma análise dinâmica tendo em conta a teoria de segunda ordem. Die Normalkräfte Ni in den einzelnen Geschossen i = 1…n ergeben sich aus den Vertikalkräften in der Bemessungssituation Erdbeben (siehe Gleichung 2). Die Geschosshöhe ist mit hi definiert.
![Redução de um edifício a uma estrutura cantilever. Os pontos de massa individuais representam os pisos. A flecha devido às forças de compressão normais mostradas em (a) é (b) convertida em momentos equivalentes de deslocamento ou forças de corte [2]]](/pt/webimage/009762/467694/01-de-png.png?mw=760&hash=85d1dbfea5c6ec9f0f573d148cc6d8ae68201a9d)
Die geometrische Steifigkeitsmatrix Kg kann über die statischen Gleichgewichtsbedingungen hergeleitet werden:
Por razões de simplificação, apenas os graus de liberdade dos deslocamentos horizontais são aqui apresentados. A derivação apresentada é baseada na abordagem do momento de desvio devido à aplicação do deslocamento linear. Esta é uma simplificação para o elemento de flexão e uma suposição exata para o elemento de treliça. Pode ser obtida uma determinação mais precisa da matriz de rigidez geométrica para vigas de flexão através da abordagem do deslocamento cúbico ou da solução analítica da equação diferencial da linha de flexão. Mais informação sobre a teoria e as derivações é fornecidas por Werkle [4]. Die geometrische Steifigkeitsmatrix Kg wird der Systemsteifigkeitsmatrix K hinzugefügt und ergibt die modifizierte Steifigkeitsmatrix Kmod:
kmod =k +kg (4)
No caso de forças axiais de compressão, isso leva a uma redução na rigidez.
Exemplo: Eigenfrequenzen und multi-modales Antwortspektrenverfahren unter Berücksichtigung der Theorie II. Ordnung
Nachfolgend wird gezeigt, wie die geometrische Steifigkeitsmatrix in RFEM und den Zusatzmodulen RF-DYNAM Pro berücksichtigt werden kann. A viga em consola apresentada na Figura 01 é utilizada como exemplo. A consola é constituída por cinco pontos de massa concentrados. Aqui, 4000 kg atuam na direção global X em cada caso.
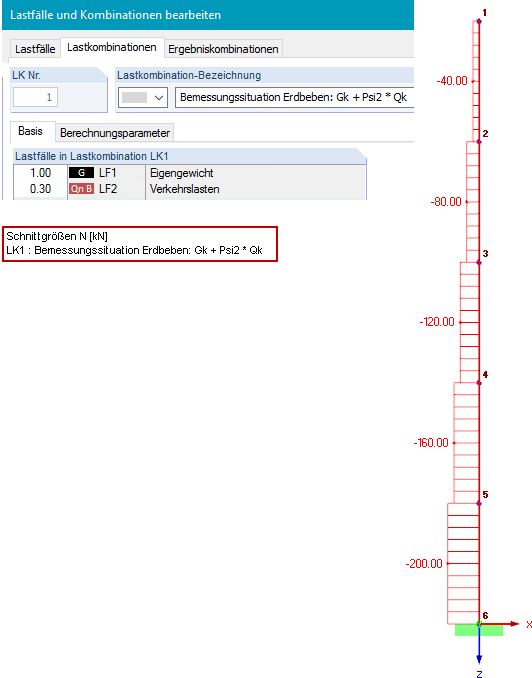
A secção é IPE 300 feita a partir do material S 235 com Iy = 8356 ∙ 10-5 m4 e E = 2,1 ∙ 1011 N/m2. Um die geometrische Steifigkeitsmatrix bei einer dynamischen Analyse berücksichtigen zu können, wird zunächst im Hauptprogramm RFEM eine Lastkombination für die Bemessungssituation Erdbeben (siehe Gleichung 2) definiert.
Mit RF-DYNAM Pro - Eigenschwingungen werden Eigenfrequenzen, Eigenformen und effektive Modalmassen einer Struktur ermittelt, dies kann unter Berücksichtigung verschiedenster Steifigkeitsmodifikationen geschehen (siehe Kapitel 2.4.7 im RF-DYNAM Pro Handbuch [5] und im Dlubal-Blog [6]). Zwei Eigenschwingungsfälle sind definiert. Im ESF2 wird die LK1 zur Berücksichtigung der geometrischen Steifigkeitsmatrix und damit zur Berücksichtigung der Theorie II. Ordnung importiert. Zum Vergleich ist der ESF1 definiert, dieser enthält keine Steifigkeitsmodifikationen.
In der nachstehenden Tabelle sind die ermittelten Eigenfrequenzen f [Hz], Eigenperioden T [sec] und die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²], mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix Kg resultierend aus den Normalkräften aus LK1, aufgelistet.
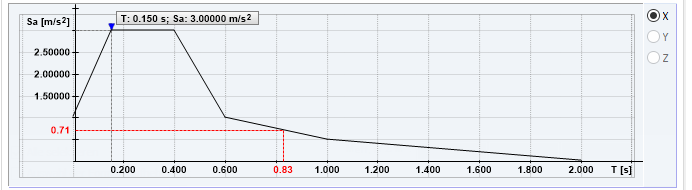
A análise do espectro de resposta multimodal utiliza frequências naturais para determinar os valores de aceleração a partir do espectro de resposta definido. Diese Beschleunigungswerte sind Grundlage für die Ermittlung der Ersatzlasten und Schnittgrößen des Antwortspektrenverfahrens. Die grafische Darstellung des benutzerdefinierten Antwortspektrums ist in Bild 6 gezeigt, die aus dem Antwortspektrum abgelesenen Beschleunigungswerte Sa [m/s²] für jeden Eigenwert sind in vorstehender Tabelle gelistet.
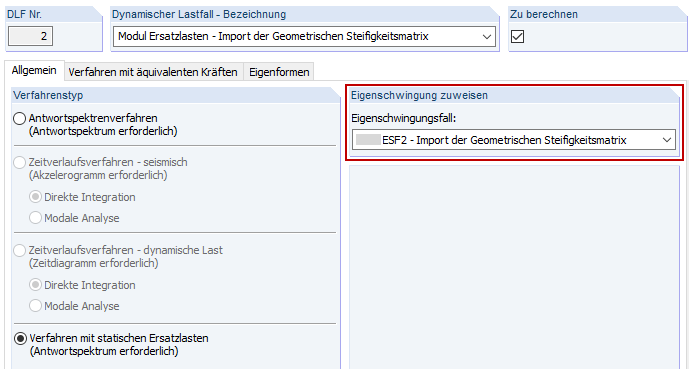
Um eine richtige Zuordnung der modifizierten Frequenzen sicherzustellen, muss der richtige Eigenschwingungsfall (ESF) im Dynamischen Lastfall (DLF) zugewiesen werden.
No caso de forças axiais de compressão, a consideração da matriz de rigidez geométrica leva à redução da frequência natural e pode causar valores de aceleração Sa mais baixos, como no nosso exemplo. Apenas uma modificação das frequências naturais não é suficiente para considerar a teoria de segunda ordem. Na verdade, isto pode na verdade levar a resultados inferiores, o que pode estar incorreto. É muito importante que a matriz de rigidez modificada também seja utilizada para a determinação das forças internas e das deformações. In RF-DYNAM Pro - Erzwungene Schwingungen wird die modifizierte Steifigkeit automatisch zur Ermittlung der Ergebnisse des Antwortspektrenverfahrens verwendet, da hier die Berechnung innerhalb von RF-DYNAM Pro stattfindet. In RF-DYNAM Pro - Ersatzlasten werden Ersatzlasten ermittelt und in Lastfälle ins Hauptprogramm RFEM exportiert. Die Berechnung findet damit teilweise in RF-DYNAM Pro und teilweise in RFEM statt. Theoretische Hintergründe zur Berechnung der Ersatzlasten finden sich im RF-DYNAM Pro Handbuch [5]. Ein Verifikationsbeispiel [7] zeigt die Berechnung an einem konkreten Beispiel. Die ermittelten Ersatzlasten, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 8 dargestellt.
Der Export der Ersatzlasten hat viele Vorteile, aber eine korrekte Übernahme der Steifigkeitsmodifikation in die Lastfälle ist wichtig. Die Berechnungsparameter der exportierten Lastfälle müssen, wie in Bild 9 gezeigt, modifiziert werden.
Die einzelnen Lastfälle werden mit der SRSS- oder CQC-Regel überlagert. Dies wird automatisch von RF-DYNAM Pro gesteuert und in Ergebniskombinationen exportiert. Die Ergebnisse, mit und ohne Berücksichtigung der geometrischen Steifigkeitsmatrix, sind in Bild 10 dargestellt.
A consideração da matriz de rigidez geométrica leva a deformações e esforços internos maiores. Die angreifenden Ersatzlasten und resultierenden Auflagerlasten hingegen sind etwas kleiner unter Berücksichtigung der geometrischen Steifigkeitsmatrix.