Les surfaces ayant uniquement les directions x et y dans le plan, il est nécessaire de définir la contrainte circonférentielle et la contrainte normale. Dans l’exemple suivant, sigma_x doit être la contrainte normale et sigma_y la contrainte circonférentielle.
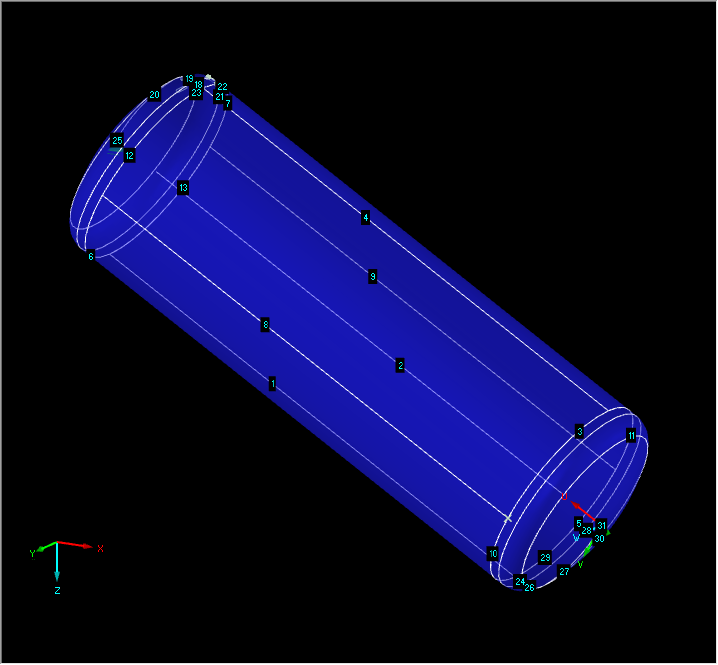
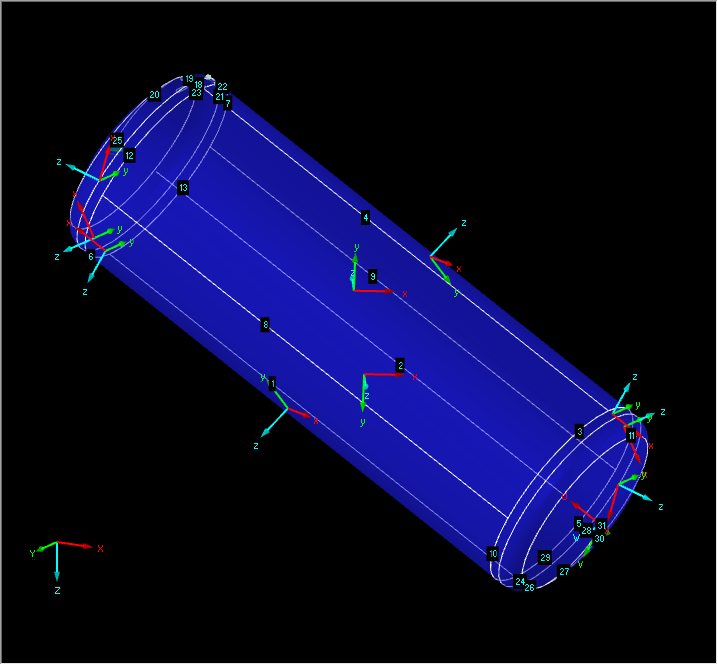
Le modèle est un conteneur circulaire incliné (Figure 01). Après la modélisation, le logiciel essaie d’aligner les systèmes d’axes locaux sur les systèmes d’axes globaux (Figure 02). Dans le cas présent, l’axe x doit cependant s’étendre le long du conteneur pour toutes les surfaces. Cette orientation peut être obtenue de la manière décrite ci-dessous.
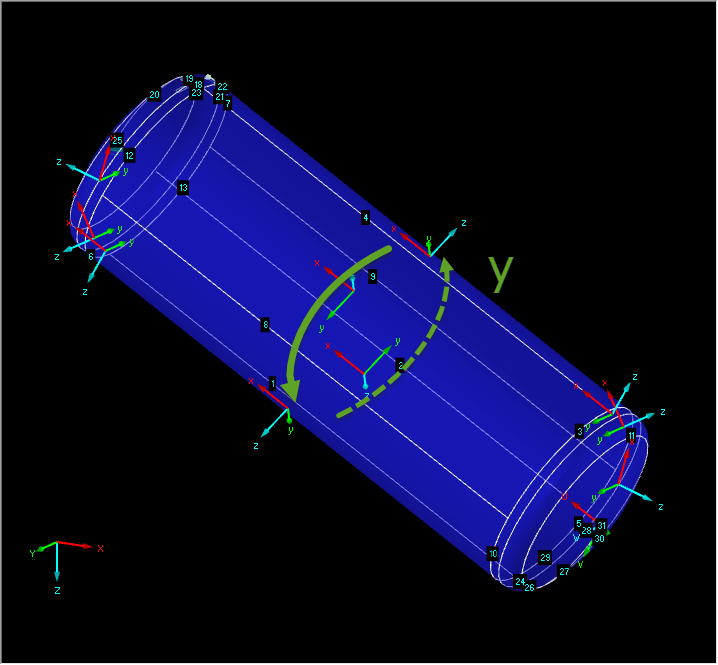
L’axe z de toutes les surfaces doit tout d'abord pointer vers l’intérieur ou l’extérieur. Dans cet exemple, la direction extérieure a été sélectionnée. Si ce n'est pas le cas pour une surface, vous pouvez déplacer l'axe z de l'autre côté de la surface par un clic-droit sur la surface et en utilisant la fonction « Inverser le système d’axes local ». Sélectionnez ensuite toutes les surfaces et cliquez sur l’onglet Axes dans la boîte de dialogue des surfaces. La Figure 03 montre cette boîte de dialogue. Dans cet exemple, l’une des lignes de contour s'étendant axialement a été sélectionnée pour l’orientation. La Figure 04 montre les systèmes d’axes locaux une fois alignés. Tous les axes x s’étendent axialement et tous les axes y sont dans la direction circonférentielle.
La Figure 05 montre les résultats des contraintes normales de membrane (sigma-x, m) et des contraintes circonférentielles (sigma-y, m).