U velmi rozsáhlých modelů s velmi mnoha stupni volnosti nebo u konstrukcí, jejichž základní vlastní čísla se nacházejí ve vysokofrekvenční oblasti (například potrubní systémy), může být tento požadavek těžko splnitelný. V takových případech nabývá na významu metoda ZPA (Zero-Period-Acceleration). Tato metoda také umožňuje zohlednit samotné hmoty v podporách, což má rozhodující vliv na podporové síly.
Rozlišujeme tři oblasti frekvencí, na jejichž základě se třídí odezvy konstrukce (viz obr. 01): (1) nízkofrekvenční oblast, (2) středofrekvenční oblast a (3) vysokofrekvenční oblast.
Der niederfrequente und mittelfrequente Bereich (f < fZPA) ist der in der Baudynamik üblicherweise betrachtete Bereich. Stavby mívají dominantní vlastní frekvence v této oblasti a v mnoha případech se těmito vlastními hodnotami aktivuje více než 90 % hmotnosti konstrukce. Systémové odezvy v nízkofrekvenční oblasti jsou periodické a výsledky různých vlastních čísel vykazují fázový posun. Odezvy jednotlivých vlastních hodnot se skládají do kombinací podle pravidel kvadratické superpozice SRSS nebo ještě lépe CQC.
Im hochfrequenten Bereich (f > fZPA) fallen die Systemantworten pseudo-statisch aus, die Antworten aus einzelnen Eigenwerten sind gleichphasig. Modální superpozice tak může odpovídat algebraickému součtu. Místo dynamického zohlednění těchto vysokých frekvencí se obvykle vypočítají chybějící aktivované hmoty a hodnotou ZPA se k tomu pseudostaticky zohlední odezvy celé vysokofrekvenční oblasti. Der ZPA-Wert entspricht dem Wert aus dem Antwortspektrum zur Periode T = 0 sec; ZPA = Sa(T=0). Pro ZPA se ovšem připouští také uživatelsky zadaná hodnota. Diese Methode wird als ZPA-Methode, als Missing-Mass-Methode oder auch als Statische Korrektur bezeichnet [2, 3, 4].
Frequenzen im mittleren Bereich (fSP < f < fZPA) liefern Systemantworten, die zu Teilen periodisch und zu Teilen pseudo-statisch sind. Diese Frequenzen können mit speziellen Überlagerungsvorschriften wie zum Beispiel der Gupta-Methode [2] kombiniert werden, um die algebraische Summierung der pseudo-statischen Anteile zu berücksichtigen. Kvadratická superpozice podle pravidel CQC je ovšem také běžná.
Die Frequenz fSP (sp = spectral peak) entspricht dem Maximalwert der spektralen Beschleunigung. Die ZPA-Frequenz fZPA (ZPA = Zero-Period-Acceleration) ist die minimale Frequenz mit welcher die Beschleunigung näherungsweise den ZPA-Wert erreicht.
Výpočet složek ZPA
Složky aktivovaných hmot na každém jednotlivém uzlu v systému lze spočítat následovně:
kde
i = 1...p = počet vlastních čísel zohledněných při analýze spektra odezvy
j = směr seizmického buzení
mj = (mX,j, mY,j, mZ,j) = Anteile der aktivierten Massen an jedem Knoten in Anregungsrichtung j
Γij = podílové součinitele pro vlastní číslo i a směr buzení j
ui = (uX, uY, uZ)T = Eigenform des Eigenwertes i an einem einzelnen Knoten, massenormiert mit Mi = uiT ∙ M ∙ ui = 1 kg
Složka chybějících, neaktivovaných hmot na každém jednotlivém uzlu odpovídá rozdílu celkové hmoty konstrukce a aktivovaných hmot a stanoví se následovně:
mj,missing = 1 - mj
Náhradní zatížení na každém uzlu a z nich plynoucí deformace a vnitřní síly pro složku neaktivovaných hmot určíme ze vztahu:
Fj = mj,missing ∙ ZPAj ∙ M
kde
Fj = (FX,j, FY,j, FZ,j) = Ersatzlasten an jedem Knoten für den Anteil der nicht aktivierten Massen, resultierend aus der Anregungsrichtung j
ZPAj = spektrale Beschleunigung Sa,j(T=0) in Richtung der Anregung j
M = (MX, MY, MZ) = Masse an den einzelnen Knoten im System
K takto vypočítaným výsledkům složek ZPA přistupujeme při modální superpozici jako k dalšímu vlastnímu číslu. Superponovat je lze s výsledky dynamicky uvažovaných vlastních čísel podle pravidla SRSS nebo jako absolutní součet. V případě absolutního součtu jsou výsledky na straně bezpečnosti.
Použití v modulu DYNAM Pro – Forced Vibrations
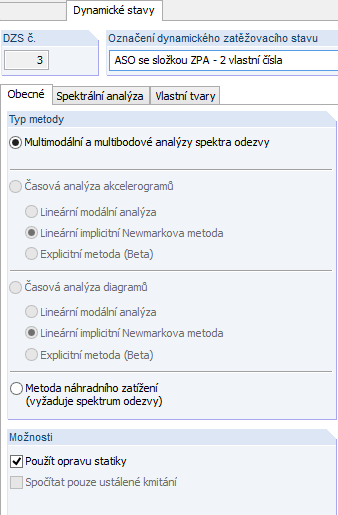
In DYNAM Pro - Erzwungene Schwingungen wird die ZPA-Methode angewendet, wenn das Kontrollkästchen "Statische Korrektur anwenden" selektiert ist. Die Einstellung ist in Bild 02 dargestellt.
V modulu DYNAM Pro se neaktivované hmoty a z nich plynoucí náhradní zatížení vypočítají interně v programu. Der ZPA-Wert ist definiert mit dem Wert aus dem Antwortspektrum zur Periode T = 0 sec; ZPA = Sa(T=0). Výsledky složky ZPA se superponují s výsledky dynamicky zohledněných vlastních čísel jako absolutní součet.
Rt = |RSRSS/CQC| + |Rmissing|
kde
Rt = Ergebnisse nach modaler und direktionaler Überlagerung inklusive dem ZPA-Anteil
RSRSS/CQC = Ergebnisse der dynamisch berücksichtigten Eigenwerte, modal überlagert mit der SRSS-oder der CQC-Regel
Rmissing = Ergebnisse des ZPA-Anteiles
Výsledky se po provedené superpozici převedou jako kombinace výsledků do hlavního programu RSTAB.
Příklad použití
Na konzole s pěti stupni volnosti si ukážeme, jak se v modulu DYNAM Pro – Forced Vibrations uplatňuje metoda ZPA. Pro naši analýzu jsme zvolili velmi jednoduchou konstrukci, abychom mohli výsledky snadno překontrolovat. Gewählt ist ein steifer Querschnitt RO 508,0x10,0 mit Iy = 48.520 cm4 aus Stahl S 235, um Frequenzen oberhalb des Wertes fZPA mit relevanter Massenbeteiligung zu erzielen. Vlastní tíha nosníku, která činí 612,3 kg, se rovnoměrně rozloží na šest uzlů (včetně uzlu s podporou). Dodatečně zadáme hmotu 1 t na uzlu 5. Hmoty i buzení konstrukce působí ve směru X. Konstrukce s rozdělením hmot, výslednými vlastními frekvencemi a účinnými modálními hmotami je spolu s uživatelsky zadaným spektrem odezvy znázorněna na Obr. 03.
In diesem Beispiel ergibt sich der ZPA-Wert zu Sa = 2,00 m/s2. Jedná se o hodnotu zrychlení při periodě T=0 s. Stellt man das Antwortspektrum gegenüber den Frequenzen dar, ergibt sich durch Grenzwertbetrachtung die Frequenz fZPA mit 100 Hz. Die ersten beiden Frequenzen f1 = 19,8 Hz und f2 = 92,8 Hz liegen somit im mittleren Frequenzbereich (siehe Bild 01) und werden dynamisch berücksichtigt. Ostatní tři vlastní frekvence jsou vysoké frekvence a lze je analyzovat metodou ZPA.
Při standardním nastavení se ve výpočtu vlastních čísel v modulu DYNAM Pro nezohlední hmoty na pevných podporách. Tyto hmoty nemají žádný vliv na vypočítané vlastní frekvence a pouze tímto způsobem lze dosáhnout faktorů účinných modálních hmot v součtu 100 %.
Pokud ovšem výslovně požadujeme, aby se hmoty na podporách při analýze metodou ZPA také zohlednily, musí být tyto hmoty v modulu DYNAM Pro aktivovány (viz nastavení na Obr. 04). V našem příkladu se budou hmoty na podporách uvažovat.
Aktivací volby „Zanedbávané hmoty...“ pozměníme standardní nastavení, při kterém se hmoty zohledňují. Jestliže ponecháme tabulku „Uzlové podpory“ prázdnou, budou se uvažovat také hmoty na podporách.
In der folgenden Tabelle werden die Beteiligungsfaktoren ΓX, die Anteile der aktivierten Massen mX, die Anteile der nicht aktivierten Massen mX,missing und die resultierenden Ersatzlasten an den sechs Knoten im System ermittelt. Základy výpočtu metodou ZPA jsme popsali výše.
| Uzel | Hmotnost Mx | součinitel kombinace ΓX | Vlastní tvar uX | Anteile der aktivierten Hmotnosti mX | Anteile der fehlenden Hmotnosti mX,missing | Náhradní břemena fX [N] | ||
| Form 1 | Form 2 | Form 1 | Form 2 | |||||
| 1 | 61,23 | 0,078350 | -0,056290 | 0,3220 | 0,6780 | 83,03 | ||
| 2 | 122,46 | 0,056790 | -0,008520 | 1,1325 | -0,1325 | -32,44 | ||
| 3 | 122,46 | 24,12 | 27,85 | 0,036140 | 0,027190 | 1,6290 | -0,6290 | -154,05 |
| 4 | 122,46 | 0,018110 | 0,038290 | 1,5033 | -0,5033 | -123,26 | ||
| 5 | 1.122,46 | 0,005100 | 0,021670 | 0,7266 | 0,2734 | 613,82 | ||
| 6 | 61,23 | 0,000000 | 0,000000 | 0,0000 | 1,0000 | 122,46 | ||
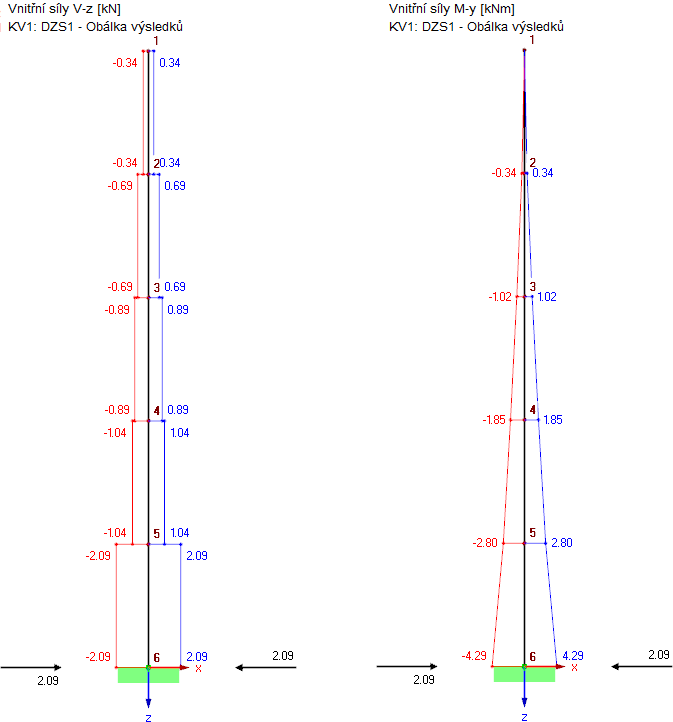
Posouvající síly, momenty a podporové síly, které plynou z těchto náhradních zatížení, jsou znázorněny na Obr. 05.
Konečné výsledky multimodální analýzy s použitím spektra odezvy a metody ZPA se stanoví z výsledných hodnot obou prvních vlastních tvarů (zde po modální superpozici podle pravidla SRSS) a z výsledků složky ZPA (viz Obr. 05).
In Bild 06 sind die Ergebnisse des Antwortspektrenverfahrens unter Berücksichtigung der ersten beiden Eigenwerte (DLF2 und EK2 im Modell) den finalen Ergebnissen inklusive dem ZPA-Anteil (DLF3 und EK3 im Modell) gegenübergestellt. Betrachtet man Bild 05 und Bild 06, ist die absolute Summenbildung, die in DYNAM Pro Verwendung findet, klar zu erkennen.
Na Obr. 07 jsou pro porovnání znázorněny výsledky analýzy spektra odezvy, při které se zohledňuje všech pět vlastních čísel. Při použití metody ZPA se uvažují hmoty na podporách. Dadurch ergibt sich eine größere Auflagerkraft PX = 2,57 kN. Vnitřní síly jsou na straně bezpečnosti, protože pro superpozici jsme uplatnili absolutní součet (srovnej Obr. 07 s Obr. 06).
Závěr
Na tomto příkladu jsme předvedli, jak se metoda ZPA uplatňuje v modulu DYNAM Pro, a ukázali jsme, že výsledky lze spolehlivě ověřit. Tuto metodu lze doporučit v případě, kdy vysoké frekvence konstrukce aktivují relevantní podíly hmot a kdy stavba vykazuje větší množství hmot na podporách.
![Spektrale Beschleunigung Sa [m/s²] versus Eigenfrequenz f [Hz] eines schmalbandigen Antwortspektrums nach EN 1998-1 [1]](/cs/webimage/009251/2417756/01-cs-png.png)